Problema 444
Siga un triangle 
. Calculeu la probabilitat que en escollir a l’atzar un punt
en el seu interior, aquest punt diste menys d’algun dels vèrtex del triangle
que de l’incentre I del triangle. Expresseu el resultat exclusivament en funció
de les raons trigonomètriques dels angles del triangle.
Solució:
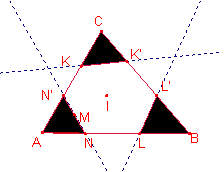
Els casos possibles és l’àrea del triangle :
. 
. 
Els punts que equidisten del vèrtex A i l’incentre I
pertanyen a la mediatriu del segment 
, la qual determina dos semiplànols, el semiplànol que conté
el vèrtex A, els seus punts estan a menor distància de A que de I.
Siga M el punt mig del segment .
La mediatriu talla els costats del triangle en els punts
N, N’.
Els casos favorables d’estar més a prop de A que de I és
l’àrea del triangle 
.
Calculem la seua àrea:
.
. 
.
.
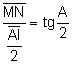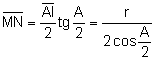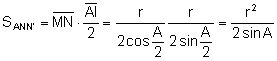Anàlogament calcularíem l’àrea dels altres triangles 
, 
els punts dels quals estan a menor distància dels vèrtexs B i
C que de I.
La probabilitat del problema és:
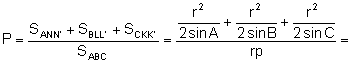
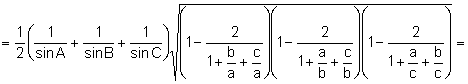
Aplicant el teorema dels sinus:
