Problema
444
Sea un triángulo 
. Hallar la probabilidad de que escogido
al azar un punto en su interior, dicho punto diste menos de alguno de los
vértices del triángulo que del incentro I del mismo.
Expresar el resultado exclusivamente en función de razones trigonométricas de
los ángulos del triángulo
Solución
de Ricard Peiró:
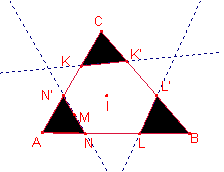
Los
casos posibles es el área del triángulo :
. 
. 
Los
puntos que equidistan del vértice A y del incentro I pertenecen
a la mediatriz del segmento 
, que determina dos semiplanos, el semiplano que contiene el vértice
A, sus puntos están a menor distancia de A que de I.
Sea
M el punto medio del segmento .
La mediatriz
corta los lados del triángulo en los puntos N, N’.
Los
casos favorables de estar más cerca de A que de I es el área del triángulo 
.
Calculemos
su área:
.
. 
.
.
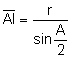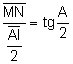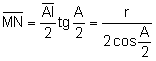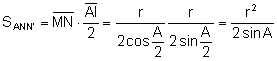Análogamente
calcularíamos el área de los otros triángulos 
, 
tal que los están a
menor distancia de los vértices B y C que de I.
La probabilidad
del problema es:
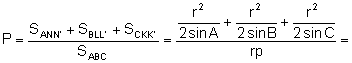
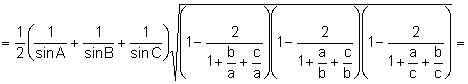
Aplicando
el teorema de los senos:
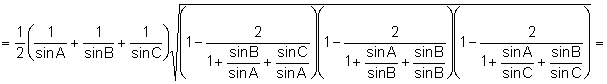
