Problema 444

Sea un triángulo ABC. Hallar la probabilidad de que escogido al azar un punto en su interior, dicho punto diste menos de alguno de los vértices del triángulo que del incentro I del mismo. Expresar el resultado exclusivamente en función de razones trigonométricas de los ángulos del triángulo.

Propuesto por Vicente Vicario García, I.E.S. “EL SUR”, Huelva).

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Utilizaremos la notación habitual en la geometría del triángulo. Sea P el punto escogido al azar en el interior del triángulo e I el incentro del mismo. Obviamente I es interior al triángulo. Consideremos los segmentos AI, BI, CI que unen el incentro con cada uno de los vértices del triángulo y los segmentos A´A´´, B´B´´, C´C´´ perpendiculares a los anteriores por sus puntos medios. Estos últimos segmentos se cortan, dos a dos, siempre en el exterior del triángulo puesto que se tiene fácilmente que

, , y los triángulos BIA, BIC y CIA son obtusángulos con circuncentros exteriores a los mismos.

Dados dos puntos en el plano, como el incentro I del triángulo y un vértice del mismo, como por ejemplo A, sabemos que un punto P dista menos de A que de I siempre que pertenezca al semiplano infinito contiguo a A que determina la mediatriz del segmento AI. La probabilidad pedida en nuestro problema será entonces el cociente que resulta de sumar las áreas de los triángulos AA´A´´, BB´B´´ y CC´C´´ entre el área del triángulo ABC.

Para efectuar este cálculo necesitamos emplear un lema, que demostramos

Lema1: “Para todo triángulo ABC se tiene que donde R es el radio de la circunferencia circunscrita al triángulo y r el radio de la circunferencia inscrita al mismo”.

Demostración: Utilizando sucesivamente identidades trigonométricas muy conocidas tenemos la siguiente identidad

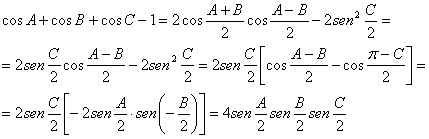
Por otra parte, deduciremos una serie de relaciones relacionadas con los cosenos de los ángulos del triángulo dado. En particular el valor de en función de R y r. Sea A un ángulo del triángulo, demostraremos entonces que cosA es una raíz real de la ecuación polinómica siguiente:

Para la demostración consideremos las relaciones (teorema de los senos generalizado) y (relacionada con el incentro). Utilizando las identidades trigonométricas del ángulo doble, tenemos que

Elevando al cuadrado y operando se tiene

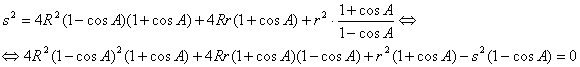
de donde, después de manipulaciones algebraicas, llegamos a la relación que queremos

Claramente esta relación se cumple también para y . De las relaciones de Cardano-Vieta entre las raíces y los coeficientes deducimos las relaciones

[1]

Observando la primera de las expresiones de [1] y lo demostrado al comienzo del lema, tenemos demostrado el mismo. ■

Considerando uno de los tres triángulos verticiales como el triángulo AA´A´´ es inmediato que es isósceles. Si denotamos x a la longitud de la mitad de su base A´A´´ y puesto que a aplicando el lema anterior se obtiene inmediatamente que

, ,

entonces

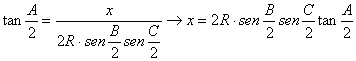
y su área viene dada por

y expresiones análogas para las área de los triángulos y .

Por otra parte, utilizando el teorema de los senos generalizado, podemos expresar el área del triángulo en la forma

La probabilidad pedida, después de simplificaciones evidentes será entonces

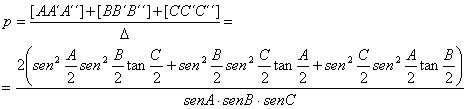
[2]

Nota: Como corolario de la solución del problema, podemos observar que puesto que la probabilidad p cumple las desigualdades , entonces de [2], tenemos asegurado que en todo triángulo se cumple la desigualdad siguiente

desigualdad, en principio, nada obvia.

---oooOooo---