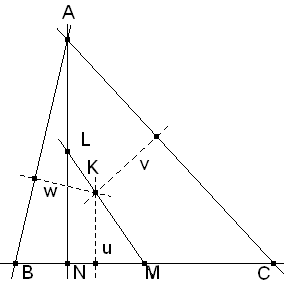
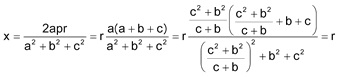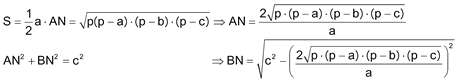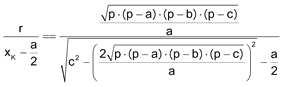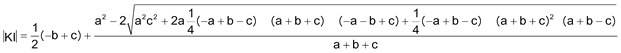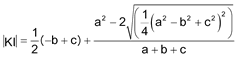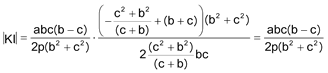De investigación.Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 445.

Si el lado a de un triángulo ABC es igual al cociente de la suma de los cuadrados de los otros dos lados por la suma de estos lados, la recta KI que une el punto de Lemoine al centro del círculo inscrito, es paralela a aquel lado e igual a

,

siendo p el semiperímetro.

De Alba , L. (1901): Revista Trimestral de Matemáticas , Año I, pp.139-142, Diciembre, (número 4) (Problema 375)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (3 de marzo de 2008)

SOLUCIÓN

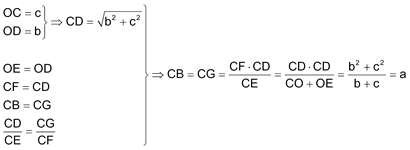
Usaremos dos propiedades del punto K, sin demostración por encontrarse abundantemente en la literatura.

“ Las distancias de K a los lados son proporcionales a dichos lados.“

”El punto K está en la recta que une el punto medio de un lado y el punto medio de la altura a ese lado.”

PARALELISMO

Escribiendo que

nos queda

.

Es decir, la distancia de K al lado a es igual a r el radio del círculo inscrito; pero esa es la distancia del incentro I al lado a y por lo tanto KI es paralela al lado a.

DISTANCIA

Como la altura de K sobre a es r y el punto medio del lado es a/2 tenemos que

pero como

nos queda

y como la abscisa del incentro es la del punto de contacto de a con el círculo inscrito, tenemos

de donde

y como

entonces

y simplificando

nos queda

e introduciendo ahora la condición

nos queda

como nos pide el enunciado.

CABRI-COMPROBACIÓN

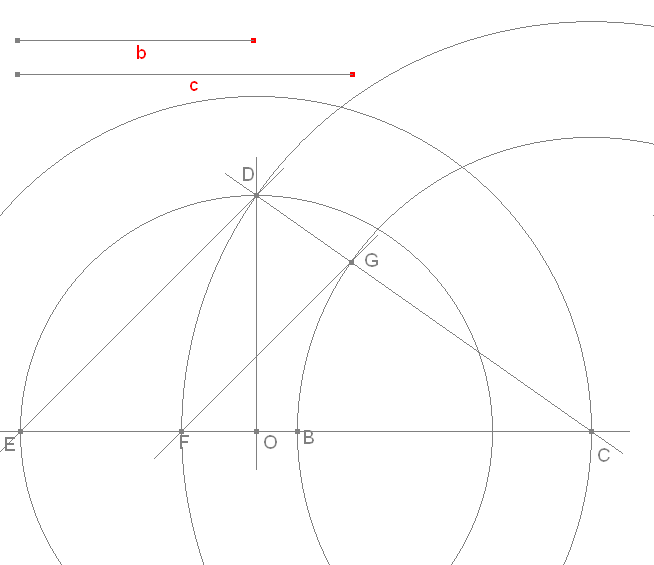
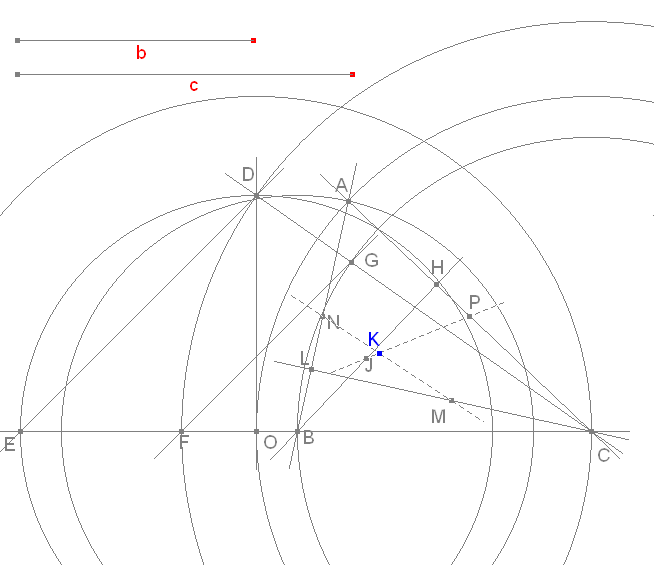
Construimos a

Construimos el punto K a través de la segunda propiedad

La altura desde B tiene su punto medio en J y la altura desde C tiene su punto medio en M. El punto medio de AB es N y el de AC es P. PJ y MN se encuentran en K.

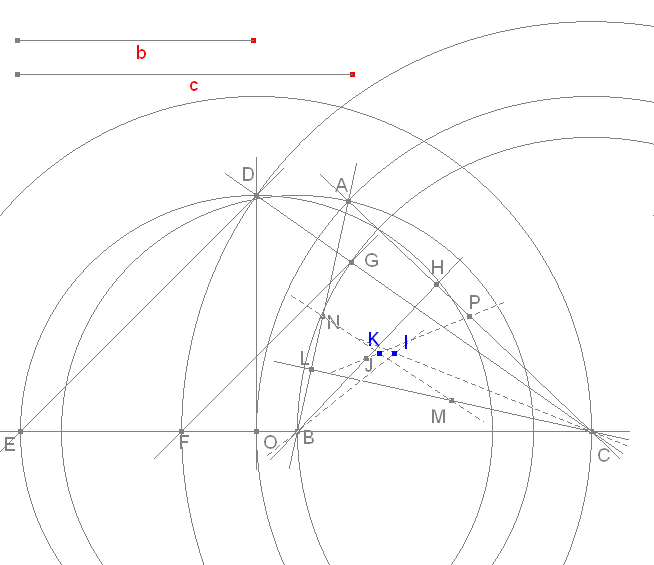
Construimos I por medio de la intersección de las bisectrices

Comprobamos el paralelismo con la figura dinámica que sigue

puede mover los elementos en rojo

puede mover los elementos en rojo