Problema 445

Problema 445.- (Propuesto por J. B. Romero Márquez, profesor colaborador de la Universidad de Valladolid).

Si el lado a de un triángulo ABC es igual al cociente de la suma de los cuadrados de los otros lados por la suma de estos lados, la recta KI que une el punto de Lemoine al centro de la circunferencia inscrita al triángulo, es paralela a aquel lado e igual a

donde s es el semiperímetro.

De Alba, L. (1901). Revista trimestral de Matemáticas. Año I. pp. 139-142. Diciembre (número4). Problema 375.

Resolución: (Vicente Vicario García, I.E.S. El SUR, Huelva)

Emplearemos la notación habitual en la geometría del triángulo. Denotaremos por D, E, F, G los pies sobre el lado BC de la mediana, bisectriz interior, simediana y altura que parten del vértice A, respectivamente. Denotaremos también al área del triángulo ABC y s al semiperímetro. Además [XYZ] representará también el área del triángulo XYZ.

Para la resolución del problema necesitamos previamente tres lemas que demostramos a continuación

Lema 1: “En un triángulo ABC y con la notación habitual, sea AF la simediana que parte del vértice A. Entonces se verifica la relación ”. (Teorema de las simedianas).

Demostración: Sean y .. Las áreas de los triángulos ABF y CAF valen

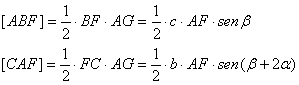
y dividiendo entre sí las relaciones anteriores tenemos que

[1]

Además, por ser AD la mediana, las áreas de los triángulos ADB y ADC son iguales, y por tanto

[2]

y sustituyendo [2] en [1] resulta

■

Lema 2: “Sea un triángulo ABC y sean AL, BM, CN tres cevianas concurrentes en P. Entonces se cumple la relación (Teorema de Von Aubel)

Demostración: Denotaremos por [XYZ] el área del triángulo XYZ. Los triángulos CAP y ABP tienen en común la base AP. La razón de sus áreas es la de sus alturas, y a su vez es la misma que la de las hipotenusas CL y BL de los dos triángulos rectángulos semejantes formados al trazar estas alturas. Entonces

[3]

De forma análoga, razonando sobre los triángulos BCP y ABP, tenemos que

[4]

De aquí se deduce que

[5]

Por otra parte, y por razones similares, tenemos que: , junto con , de donde a partir de [5] tenemos que

■

Lema 3: “ Sea un triángulo ABC y sea AE la bisectriz interior que parte del vértice A. Entonces se tiene que ”.

Demostración: Sea E el punto de corte de la bisectriz interior que parte del vértice A con el lado BC. Por el teorema de las bisectrices, denotando , podemos plantear la relación

Aplicando el teorema de los cosenos al triángulo AEB y al triángulo ABC entonces

■

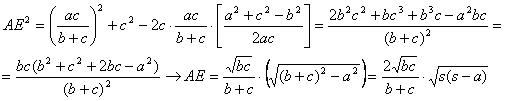Centrándonos ya en nuestro problema y con la notación habitual, demostraremos que siendo K el punto de Lemoine o punto de corte de las simedianas (punto de Grebe o simediano) entonces se tiene la relación siguiente

Esto se demuestra fácilmente a partir de los lemas 1 y 2 previos. A partir del lema 1 tenemos que

Análogamente se tiene que . A partir del lema 2 concluimos que siendo el punto , el punto de Lemoine, entonces se tiene

[6]

Es evidente que la distancia del incentro I del triángulo al lado BC es r, radio de la circunferencia inscrita. La distancia del punto de Lemoine al lado BC se puede determinar por semejanza de triángulos. Se obtiene fácilmente la relación

donde AF es la simediana que parte de A y la altura desde el mismo vértice, es decir, AG. Entonces a partir de [6] tenemos que

y por tanto

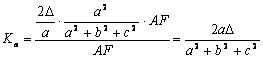[7]

Supongamos ahora, según la hipótesis del problema que . Entonces demostraremos que KI // BC ya que la distancia del punto de Lemoine K al lado BC en estas circunstancias es exactamente igual al radio r de la circunferencia inscrita. A partir de la expresión anterior llegamos, después de simplificar a la igualdad

y por tanto, resulta que KI // BC. Para obtener la expresión de KI, aplicando el teorema de las bisectrices interiores y la demostración del lema 3 tenemos que

y como , entonces , con lo que según el lema 3 entonces tenemos que

Finalmente, puesto que KI // BC, por semejanza de triángulos tenemos fácilmente que

y como , entonces

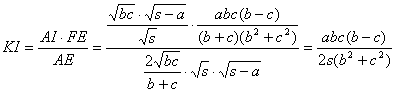
Nota 1: El triángulo tal que cumple otras varias propiedades interesantes. Algunas de ellas pueden verse en los artículos “Triángulos especiales II y III” de D. Francisco Bellot Rosado, de la revista digital de la OIM. Podemos resumir algunas propiedades de este triángulo:

(a) La simediana desde A pasa por el punto de tangencia de la circunferencia inscrita con el lado BC.

(b) Las rectas AI y CJ (J, punto de tangencia de la circunferencia inscrita con AB), se cortan sobre la mediana BM.

(d)

(e)

(f)

(g)

(h)

Nota 2: El teorema recíproco al dado también es cierto. Es decir, si en un triángulo ABC se tiene que KI // BC entonces se verifica que. La demostración es relativamente sencilla ya que si KI // BC , y como

(que ya hemos demostrado anteriormente), entonces

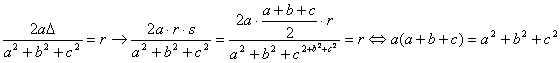
lo que implica entonces que .