Para el aula

Problema 446

D, E y F son los puntos medios de los lados BC, CA y AB de un triángulo. Una recta cualquiera que pase por A corta a las rectas DE y DF en G y H. Demostrar que CG es paralela a BH.

Aref, M.N., Wernick,W. (1968): Problems &Solutions in Euclidean Geometry. Dover Publications, Inc, New York. (pag. 59) (43)

Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fenlabrada

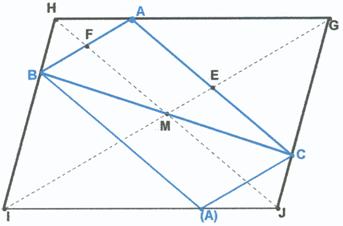
Comencemos por el problema resuelto. Sea un paralelogramo GHIJ de centro M. Si se tomara un punto cualquiera A en el lado HG como vértice del paralelogramo AB(A)C inscrito en el paralelogramo GHIJ y cuyos lados sean paralelos a las diagonales se cumple:

· M es el centro de los dos paralelogramos luego es el centro de la diagonal BC del paralelogramo inscrito.

· El lado AB y la diagonal HJ se cortan en el punto F. Este punto es el punto medio del lado AB por la homotecia de los triángulos BAH e IGH

· Por lo mismo E es el punto medio del lado AC

Luego el triángulo ABC formado por tres de los vértices del paralelogramo inscrito cumple las propiedades del triángulo dado en el problema.