Problema 446

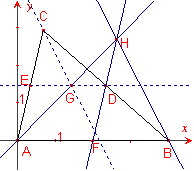
D, E, F són els punts migs dels costats d’un triangle. Una recta qualsevol que passe per A talla les rectes DE i DF en els punts G, H, respectivament. Demostreu que la recta CG és paral·lela a la recta BH.

Solució 1:

Considerem el triangle en les següents coordenades cartesianes:

.

Siga r una recta qualsevol que passa pel punt A i no passa per B, C:

, .

Els punts mig dels costats tenen coordenades:

.

La recta que passa per D, E té equació: .

La recta que passa per D, F té equació: .

H és la intersecció de les rectes r, . Les coordenades són: .

G és la intersecció de les rectes r, . Les seues coordenades són: .

.

.

Els vectors . Són linealment dependents, per tant, la recta CG és paral·lela a la recta BH.

Solució 2:

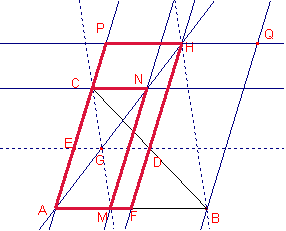
La recta CG talla el costat en el punt M.

Considerem al paral·lelogram AMNC.

Notem que G és el punt mig de , aleshores, G pertany a les dues diagonals.

Aleshores, el punt N està en la recta AM.

Considerem el paral·lelogram AFHP.

Els paral·lelograms AMNC, AFHP són homotètics i A centre de l’homotècia.

Considerem el paral·lelogram FBQH.

Els paral·lelograms AFHP i FBQH i traslladats són iguals, .

Les diagonals dels paral·lelograms AMNC, FBGH són paral·leles.

Aleshores, que la recta CG és paral·lela a la recta BH.