Problema 446

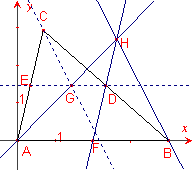
D, E y F son los puntos medios de los lados BC, CA y AB de un triángulo. Una recta cualquiera que pase por A corta a las rectas DE y DF en G y H. Demostrar que CG es paralela a BH.

Aref, M.N., Wernick,W. (1968): Problems &Solutions in Euclidean Geometry. Dover Publications, Inc, New York. (pag. 59) (43)

Solución 1 Ricard Peiró:

Consideremos el triángulo con las siguientes coordenadas cartesianas:

.

Sea r una recta cualquiera que pasa por el punto A y no pasa por B, C:

, .

Los puntos medios de los lados tienen coordenadas:

.

La recta que pasa por D, E tiene ecuación: .

La recta que pasa por D, F tiene ecuación: .

H es la intersección de las rectas r, . Las coordenadas son: .

G es la intersección de las rectas r, . Las coordenadas son: .

.

.

Los vectores . Son linealmente dependientes, por tanto, la recta CG es paralela a la recta BH.

Solución 2:

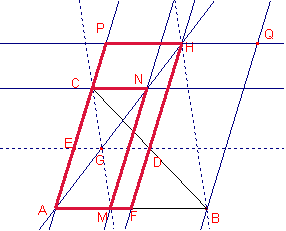
La recta CG corta el lado en el punto M.

Consideremos al paralelogramo AMNC.

Notemos que G es el punto medio de , entonces, G pertenece a las dos diagonales.

Entonces, el punto N está en la recta AM.

Consideremos el paralelogramo AFHP.

Los paralelogramos AMNC, AFHP son homotéticos y A centro de la homotecia.

Consideremos el paralelogramo FBQH.

Los paralelogramos AFHP y FBQH y trasladados son iguales, .

Las diagonales de los paralelogramos AMNC, FBGH son paralelas.

Entonces, que la recta CG es paralela a la recta BH.