Problema 446.- D,
E, F son los puntos medios de los lados BC, CA y AB de un triángulo ABC, respectivamente. Una recta cualquiera que pase por A corta a las rectas DE y DF
en G y H, respectivamente. Demostrar que CG es paralelo a BH.
Aref, M.N. Wernick, W (1968). Problems & Solutions in Euclidean Geometry.
Dover Publications, Inc,
Resolución: (Vicente Vicario García, I.E.S.
El SUR, Huelva)
Utilizaremos la geometría de
coordenadas. Sin pérdida de generalidad podemos suponer que las coordenadas de
los vértices de nuestro triángulo son 
, 
y 
. Los puntos D, E, F,
puesto que son puntos medios de los lados del triángulo tendrán como
coordenadas 
. La recta arbitraria que pasa por A, sin pérdida de generalidad se puede escribir en la forma 
, donde m es la
pendiente variable de esta recta. El punto G
resulta de la intersección de la recta DE
y de esta recta de pendiente m. Por
tanto, como
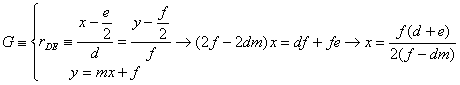
y en consecuencia 
. Así pues, las coordenadas del punto G resultan son 
.
De forma análoga determinamos las coordenadas del punto H. Entonces
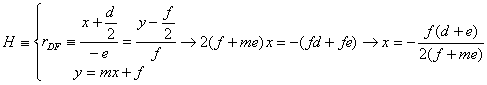
y de nuevo se tiene 
Finalmente determinamos los vectores CG y BH y comprobamos que son paralelos, es decir, tienen sus coordenadas proporcionales
que evidentemente tienen sus coordenadas proporcionales y son paralelos. Por tanto la recta CG es paralela a la recta BH.