Problema 447

Problema 5.- Sean AA 1 , BB 1 CC 1 las alturas de un triángulo acutángulo. Demostrar que los pies de las perpendiculares trazadas por C 1 a los segmentos AC, BC, AA 1 y BB 1 están alineados.

Excalibur (2007): Vol 12, n 2, Mayo-Agosto

http://www.math.ust.hk/excalibur/v12_n2.pdf

Solución de Ricard Peiró:

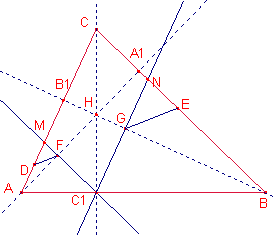Sean D, E, F, G los pies de las perpendiculares trazadas desde a los segmentos , , , .

La recta corta el lado en el punto M.

La recta corta el lado en el punto N.

Los triángulos , son homotéticos, ya que tienen Los lados paralelos.

D y F son homotéticos, E y G son homotéticos.

Los segmentos son homotéticos, entonces están sobre una recta que pasa por el centro de homotecia.