Para el aula

Problema 447

Problema 5.- Sean AA₁, BB₁ CC₁ las alturas de un triángulo acutángulo. Demostrar que los pies de las perpendiculares trazadas por C₁ a los segmentos AC, BC, AA₁ y BB₁ están alineados.

Excalibur (2007): Vol 12, n 2, Mayo-Agosto. http://www.math.ust.hk/excalibur/v12_n2.pdf

Solución.-

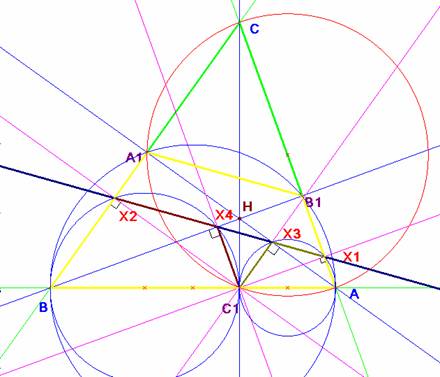
Los triángulos rectángulos BX₂C₁ y C₁X₃A son semejantes. También lo son BX₄C₁ y C₁X₁A y además tienen la misma razón de semejanza, pues

; .

luego son semejantes los triángulos X₂X₄C₁ y X₃ X₁A y a partir de eso, los cuadriláteros BX₂X₄C₁ y C₁X₃ X₁A son semejantes y de lados paralelos: son homotéticos. Además ambos son homotéticos a BA₁B₁A. En efecto BX₄C₁ y BB₁A son semejantes así como también BX₂C₁ y BA₁A, y la razón de semejanza es la misma en ambos, por tanto BX₂X₄C₁ y BA₁B₁A son semejantes y de lados paralelos. Los segmentos X₂X₄ y X₃ X₁ son ambos paralelos al segmento A₁B₁.

De otra parte, X₁X₂X₃ es la recta de Simson-Wallace del punto C₁ para el triángulo rectángulo A₁AC y por tanto X₄ está sobre ella.