Problema 447.- Sean las alturas de un triángulo acutángulo. Demostrar que los pies de las perpendiculares trazadas por a los segmentos AC, BC, y están alineados.

(Excalibur, (2007), vol 12, n2, Mayo-Agosto).

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Utilizaremos la geometría de coordenadas y el hecho bien conocido de que dos rectas en el plano son perpendiculares si y sólo si el producto de sus pendientes es -1. Sin pérdida de generalidad podemos suponer que , y . Además tenemos que , ya que el triángulo, por hipótesis, es acutángulo. Sean P y Q los puntos de corte de las rectas que partiendo de son perpendiculares a la rectas BC y AC, respectivamente. Sean M y N los puntos de corte de las rectas que partiendo de son perpendiculares a la rectas y , respectivamente. Determinemos las ecuaciones de las rectas BC y AC.

Determinemos las coordenadas del punto P. Después de un sencillo cálculo

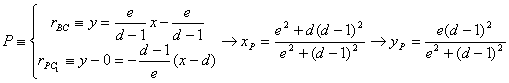
con lo que las coordenadas del punto P resultan .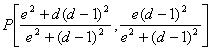

Determinemos de forma análoga las coordenadas del punto Q.

con lo que las coordenadas del punto Q resultan .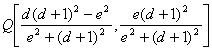

Determinemos ahora las coordenadas de los puntos M y N.

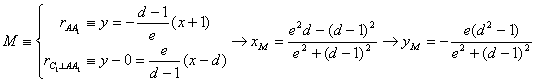con lo que las coordenadas del punto M resultan .

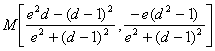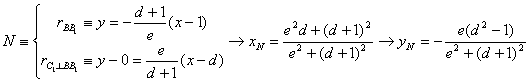con lo que las coordenadas del punto N resultan .

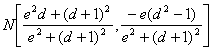Calculamos ahora la ecuación de la recta que pasa por P y M, y comprobamos después que los puntos N y Q , con lo que se termina el problema.

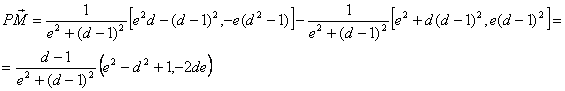
con lo que como vector director de la recta vale . Por tanto, después de manipulaciones algebraicas llegamos a que la ecuación de la recta es

Finalmente, un cálculo bastante laborioso demuestra que los puntos Q y N cumplen la ecuación de la recta , y por tanto, pertenecen a la misma.

De forma análoga tenemos que