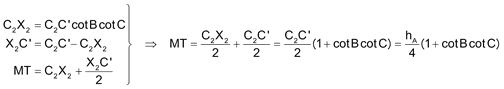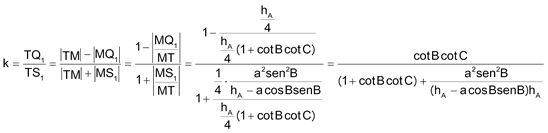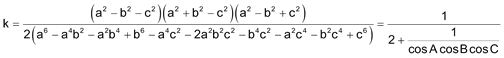|
De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid. Problema 448 Sea A'B'C' el triángulo formado con los puntos medios del triángulo dado ABC.Denotamos por Oi, Gi, Xi, i = 1, 2, 3, los circuncentros, baricentros y ortocentros de los triángulos AB'C', BC'A' y CA'B', respectivamente. Probar que: a) Los triángulos O1O2O3, G1G2G3, y X1X2X3 son semejantes al ABC y congruentes al A'B'C'. b) Si T es el ortocentro del triángulo O1O2O3, entonces T el centro de todos los rectángulos B'C'X2X3, C'A'X3X1 y A'B'X1X2. c) Sean A2, B1 las proyecciones ortogonales de A', B', respectivamente, sobre AB ; sean B3, C2 las proyecciones ortogonales de B', C', respectivamente, sobre BC ; sean A3, C1, las proyecciones ortogonales de A', C', respectivamente, sobre AC. Llamemos Q1, Q2, Q3 a los centros de los rectángulos B'C'C2B3, C'A'A3C1 y A'B'B1A2, respectivamente, y llamemos S1, S2, S3 a los puntos de intersección S1= A2C2 ∩ A3B3, S2= B1C1 ∩ B3A3 y S3 = C1B1 ∩ C2A2. Demostrar que los triángulos Q1Q2Q3 y S1S2S3 son semejantes por homotecia, de la que se calculará su centro y razón. d) B1C1 = 2 Q3Q2, A2C2 = 2 Q3Q1, A3B3 = 2 Q2Q1. Romero, J.B. (2007): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de marzo de 2008 |
|
SOLUCIÓN (a) |
|
|
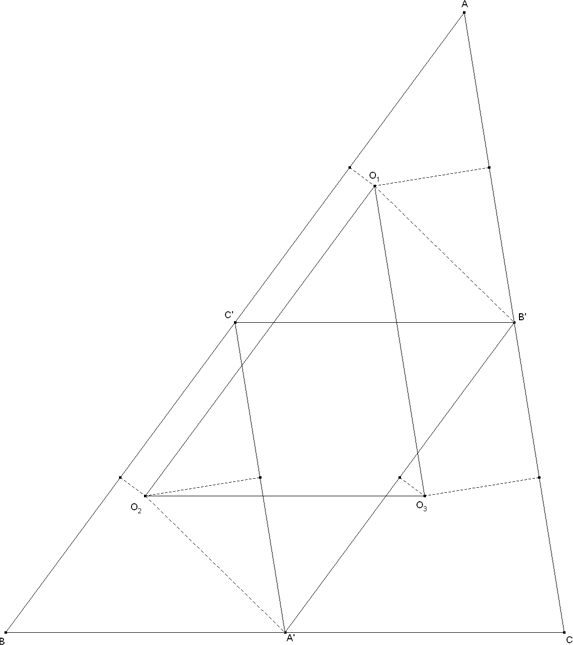
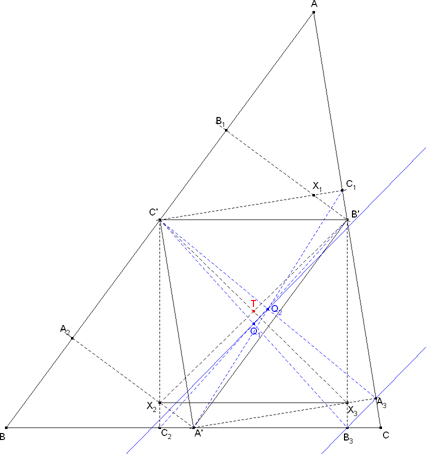
Trazamos el enunciado y por ser A', B' C' puntos medios nos queda que los triángulos AB'C', B'CA' y C'A'B son todos de lados paralelos (las rectas que unen los puntos medios de dos lados son paralelas al tercer lado). Además, como paralelas entre paralelas son iguales, podemos concluir que dichos triángulos son congruentes entre sí y semejantes al triángulo dado ABC, pues tienen los lados paralelos. También, como el triángulo A'B'C' tiene los lados paralelos a los del triángulo dado ABC y de longitud la mitad, podemos concluir que los triángulos AB'C', B'CA' y C'A'B son congruentes al triángulo A'B'C'.
Si construimos ahora los puntos Oi como intersección de las mediatrices, como las mediatrices correspondientes de los distintos triángulos (que son congruentes) son paralelas e iguales entre sí; y como paralelas entre paralelas son iguales tenemos:
y análogamente para O2O3 y O3O1 Por lo tanto el triángulo O1O2O3 tiene los lados iguales y paralelos a los del triángulo A'B'C' y en consecuencia es congruente con A'B'C' y semejante con ABC.
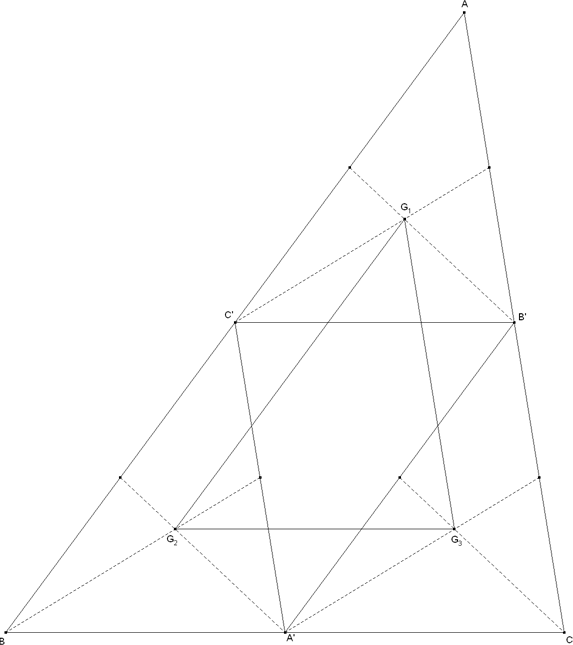
Construyendo los puntos Gi como intersección de las medianas, por el mismo motivo que en el caso de los puntos Oi, las medianas de los distintos triángulos congruentes formados son paralelas e iguales entre sí y en consecuencia:
y análogamente para G2G3 y G3G1 Por lo tanto el triángulo G1G2G3 tiene los lados iguales y paralelos a los del triángulo A'B'C' y en consecuencia es congruente con A'B'C' y semejante con ABC.
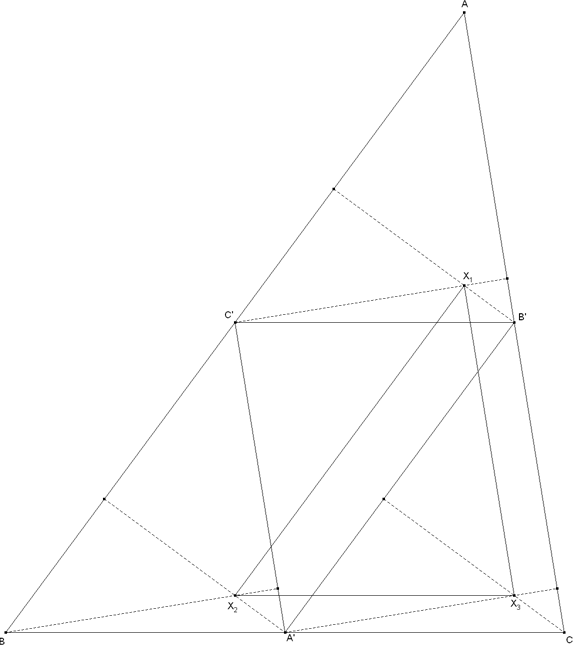
Construyendo los puntos Xi como intersección de las alturas, por el mismo motivo que en el caso de los puntos Oi y Gi, las alturas de los distintos triángulos formados son paralelas e iguales entre sí y en consecuencia:
y análogamente para X2X3 y X3X1 Por lo tanto el triángulo X1X2X3 tiene los lados iguales y paralelos a los del triángulo A'B'C' y en consecuencia es congruente con A'B'C' y semejante con ABC. |
|
SOLUCIÓN (b) |
|
|
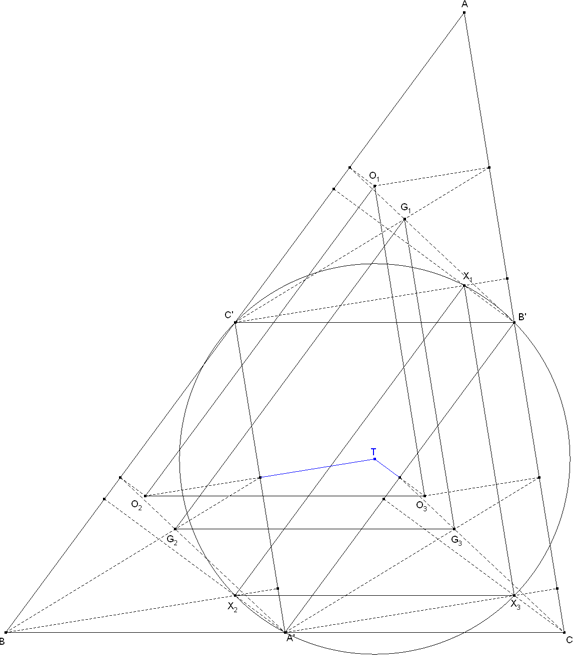
Por ser los puntos Oi intersecciones de las mediatrices de los distintos triángulos congruentes, las alturas desde los puntos Oi en el triángulo O1O2O3 son las mediatrices de los lados del triángulo A' B' C'; en consecuencia, T es el centro del círculo circunscrito al triángulo A'B'C'. Está claro que los cuadriláteros B'C'X2X3, C'A'X3X1, A'B'X1X2 (como dice el enunciado) son rectángulos por tener lados paralelos a rectas perpendiculares entre sí; en consecuencia cada conjunto de cuatro vértices son cocíclicos, lo que nos lleva a que los puntos A', B', C', X1, X2 y X3 están en el mismo círculo; y por lo tanto ese círculo es el circunscrito a A'B'C' de lo que deducimos que T es el centro de los rectángulos considerados en el enunciado. |
|
SOLUCIÓN (c) |
|
|
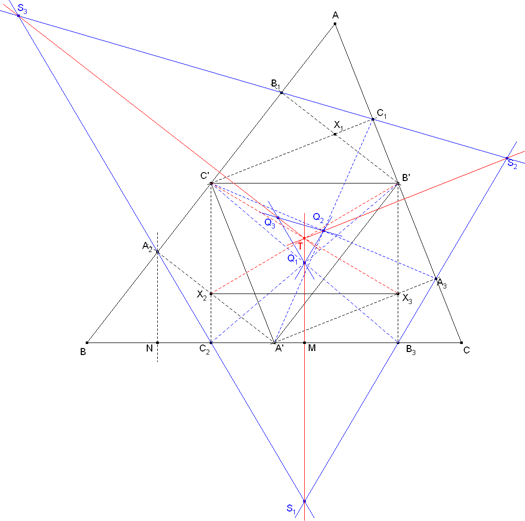
Para este apartado, basta observar que el rectángulo C'A'A3C1 es la imagen por una semejanza (giro más homotecia) de centro C' del rectángulo C'C2B3B'. Por lo tanto, A3 es la imagen por esa semejanza de B3 y por lo tanto Q2 también es la imagen de Q1 en esa semejanza; en consecuencia, Q1Q2 es paralela a B3A3 y por tanto paralela a S1S2. En particular, Q1Q2 es la imagen de B3A3 por una homotecia de centro C' y razón ½ (obtenemos esta razón por la definición de los puntos Qi como centros de los rectángulos). Análogamente Q2Q3 es paralela a S2S3 y Q3Q1 es paralela a S3S1. Concluimos pues que los triángulos Q1Q2Q3 y S1S2S3 son homotéticos.
Por otra parte Q1 es el homologo de T en la transformación que transforma el rectángulo C'B'X3X2 en el rectángulo C'B'B3B2 (TQ1 es perpendicular a BC). Pero, TS1 es perpendicular a BC (al igual que TQ1) (perpendicularidad que aquí no se demuestra); en consecuencia, la recta TQ1S1 es perpendicular a BC. De manera análoga la recta TQ2S2 es perpendicular a CA y TQ3S3 es perpendicular a AB. De lo anterior las rectas que unen los vértices homotéticos, coinciden en T por lo que T es el centro de la homotecia entre los triángulos Q1Q2Q3 y S1S2S3. Para hallar la razón de homotecia consideramos N (pie de la perpendicular desde A2 a BC) y M (punto medio de C2B3): calculamos MQ1
Calculamos MT
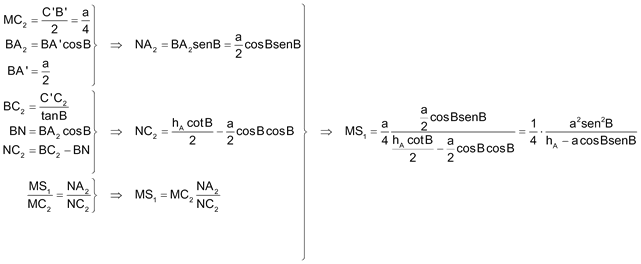
calculamos MS1
y ahora calculamos la razón k propiamente dicha
pero
y obtenemos k en función de los lados (o de los cosenos)
|
|
SOLUCIÓN (d) |
|
|
Como hemos dicho en (c), Q1Q2 es la imagen de B3A3 por una homotecia de centro C' y razón ½ y por lo tanto
Análogamente
|