De investigación.

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 448.- Sea A'B'C' el triángulo formado con los puntos medios del triángulo dado ABC.

Denotamos por O_i, G_i, X_i, i = 1, 2, 3, los circuncentros, baricentros y ortocentros de los triángulos AB'C', BC'A' y CA'B', respectivamente.

Probar que:

a) Los triángulos O₁O₂O₃,   G₁G₂G₃, y  X₁X₂X₃  son congruentes al A'B'C'.

b) Si T es el ortocentro del triángulo O₁O₂O₃, entonces T el centro de todos los rectángulos B'C'X₂X₃,  C'A'X₃X₁ y A'B'X₁X₂.

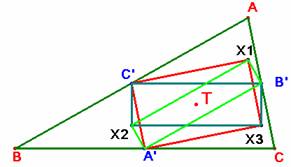
c) Sean A₂, B₁ las proyecciones ortogonales de A', B', respectivamente, sobre AB; sean B₃, C₂ las proyecciones ortogonales de B', C', respectivamente, sobre BC; sean A₃, C₁, las proyecciones ortogonales de A', C', respectivamente, sobre AC. Llamemos Q₁, Q₂, Q₃ a los centros de los rectángulos B’C’C₂B₃, C’A’A₃C₁ y A’B’B₁A₂, respectivamente, y llamemos S₁, S₂, S₃ a los puntos de intersección

S₁= A₂C₂ Ç A₃B₃, S₂= B₁C₁ Ç B₃A₃ y S₃ = C₁B₁ Ç C₂A₂.

Demostrar que los triángulos Q₁Q₂Q₃ y S₁S₂S₃ son semejantes por homotecia, de la que se calculará su centro y razón.

d)   B₁C₁ = 2 Q₃Q₂,   A₂C₂ = 2 Q₃Q₁,   A₃B₃ = 2 Q₂Q₁.

Romero, J.B. (2007): Comunicación personal.

Solución (salvo una parte de c) de Saturnino Campo Ruiz. profesor del IES Fray Luis de León, de Salamanca (7 de abril de 2008)

a) Con los puntos medios se forman tres triángulos exteriores dentro de ABC. Supongamos que tenemos un punto P del plano del triángulo ABC no situado sobre él. Trazamos desde los vértices tres rectas pasando por P. Aplicando homotecias centradas en cada uno y de razón ½, determinamos en cada triángulo exterior tres puntos P_i.

Vamos a ver que el triángulo que forman estos puntos es congruente al formado uniendo los puntos medios de los lados de ABC.

En efecto, el vector P₁P₂, es igual al vector AC’. En primer lugar tenemos, por la homotecia, AP =2AP₁, BP =2AP₂.

P₁P₂ = AP₂ - AP₁= AB + BP₂ - AP₁ = AB +½(BP-AP)= ½ AB = AC’.

Igualmente con el resto de los lados.

Sustituyendo el punto P por el circuncentro, baricentro, ortocentro, … etc. tenemos lo que queríamos.

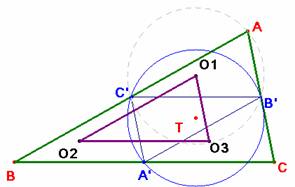
b)

O₁ está en la mediatriz de C'B'. O₂ en la de C'A' y O₃ en la de A'B', por tanto T, ortocentro de O₁O₂O₃, es el circuncentro de A'B'C'.

Sean X_i los ortocentros. La mediatriz de C'B' es la de X₂X₃. La de C'A' es la X₁X₃. Por tanto, T es el circuncentro de X₁X₂X₃.

De lo anterior se concluye que T equidista de los seis vértices A' B' C' y de los tres X_i. Por eso es el centro de los rectángulos formados con estos vértices.

d)

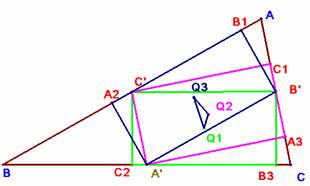
Tomando un punto cualquier O como origen de todos los vectores podemos escribir las siguientes expresiones:

OQ₁ = ½(OB’ + OC₂) = ½(OC’ + OB₃)

OQ₂ = ½(OA’ + OC₁) = ½(OC’ + OA₃)

OQ₃ = ½(OB’ + OA₂) = ½(OA’ + OB₁)

Y a partir de ellas se sigue:

Q₁Q₂ = OQ₂ - OQ₁ = ½(OA₃ - OB₃) = ½ B₃A₃

Q₁Q₃ = OQ₃ - OQ₁ = ½(OA₂ - OC₂) = ½ C₂A₂

Q₂Q₃= OQ₃ - OQ₂ = ½(OB₁ - OC₁) = ½ C₁B₁

Con esto queda probada esta parte.

c) Las expresiones obtenidas en d) demuestran la semejanza de los triángulos Q₁Q₂Q₃ y S₁S₂S₃. Girando convenientemente el triángulo inicial podemos representar la posición de estos triángulos.