Problema
448.- (`Propuesto por J. B. Romero Márquez, profesor colaborador de
Sea A´B´C´ el triángulo formado con los puntos medios del triángulo ABC. Denotamos por 
; 
, los circuncentros, baricentros y ortocentros de los
triángulos AB´C´, BC´A´ y CA´B´, respectivamente. Probar que:
(a)
Los triángulos 
, 
, 
son congruentes al triángulo A´B´C´
(b)
Si T es el ortocentro del triángulo , entonces T es el
centro de todos los rectángulos 
, 
, 
(c)
Sean 
las proyecciones
ortogonales de A´, B´ respectivamente sobre AB; Sean 
las proyecciones ortogonales de B´, C´ respectivamente
sobre BC; Sean 
las proyecciones
ortogonales de A´, C´ respectivamente sobre AC. Llamamos 
a los centros de los
rectángulos 
, 
y 
, respectivamente. Y llamamos 
a los puntos de
intersección 
, 
y 
. Demostrar que los triángulos 
y 
son semejantes por
homotecia, de la que se calculará su centro y su razón
(d)
Se cumple 
, 
y 
Resolución:
(Vicente Vicario García, I.E.S. El Sur, Huelva)
(a) Aplicando el teorema de la paralela media deducimos que
el triángulo A´B´C´ es semejante al
triángulo de partida ABC . Al trazar
las tres paralelas medias, el triángulo original queda dividido en cuatro
triángulos congruentes entre sí.
Consideremos el triángulo. Debido a la simetría es fácil ver que los lados de este
triángulo son paralelos a los lados del triángulo ABC. Además, el lado 
mide lo mismo que C´B´ (puesto que, por ejemplo, la proyección
de
sobre el segmento BA´
cae en su punto medio, etc), que según el teorema de la paralela media mide la
mitad del lado BC, y análogamente
para los otros lados. Por tanto, el triángulo es congruente al triángulo A´B´C´ debido a que tiene los tres lados iguales.
Consideremos
el triángulo. Debido a la simetría y considerando las proyecciones de
y 
sobre el lado BC, y
de y 
sobre el mismo lado,
es evidente que las distancias entre estas proyecciones alternas es la misma.
Entonces el triángulo es congruente al
triángulo A´B´C´, por el apartado
anterior.
Consideremos
el triángulo. Según el teorema de Euler, en cada triángulo se tiene
que 
, están alineados y además se cumple que 
. Por tanto, debido a la simetría y mediante una simple
traslación, vemos que el triángulo es también congruente con el triángulo A´B´C´.
(b) Claramente, y son rectángulos.
Sea T el punto de corte de las
diagonales del rectángulo. Consideremos ahora el rectángulo . Puesto que 
es una diagonal común
a los dos rectángulos, y puesto que las diagonales de un rectángulo se cortan
en su punto medio, entonces T es el
punto de corte común de las diagonales de ambos. Análogamente se demuestra con
el otro rectángulo, ya que 
es una diagonal común
a los rectángulos y .
(c) Utilizaremos la geometría de coordenadas. Usaremos el
hecho de que dos rectas en el plano son perpendiculares si y sólo si el
producto de sus pendientes es -1. Supondremos, sin pérdida de generalidad que 
, 
, 
. Entonces tenemos también que 
, 
, 
. Además tenemos las coordenadas de 
y de 
.
Determinemos
las ecuaciones de las rectas AC y AB.
Determinemos, después de
manipulaciones algebraicas, las coordenadas de los puntos
,
, 
y 
:
con lo que las coordenadas de resultan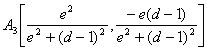 
.,
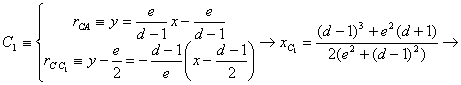
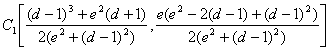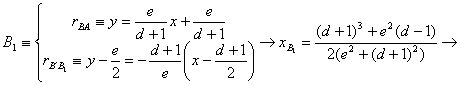
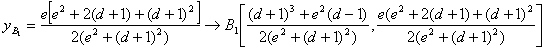
con lo que las coordenadas de resultan 
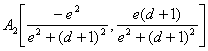
Determinemos ahora las coordenadas de los
puntos . A partir de las definiciones y de las coordenadas de los
puntos , , , 
, y
, ya calculados, es inmediato determinar que
Como
consecuencia de lo que demostraremos en el apartado (d), los lados de los
triángulos son paralelos a los
lados del triángulo y tales que son
homotéticos. Determinemos ahora las coordenadas de los puntos
y
para después hallar la razón de homotecia.
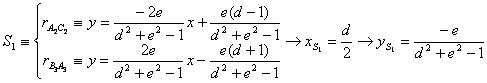
Así pues, las
coordenadas del punto resultan 
Determinemos ahora las coordenadas del punto . Necesitamos determinar el vector 
, cuyas coordenadas vienen dadas por
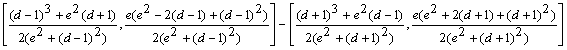
Después de manipulación algebraica tenemos que
Observando a partir de las expresiones anteriores que como
vector director de esta recta sirve 
, la ecuación de la recta que contiene el segmento viene dada por
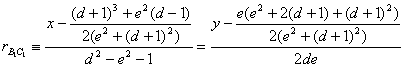
resultando, en
definitiva
Podemos ya determinar las coordenadas del punto , obteniéndose
, 
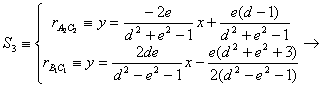
Por tanto el
vector 
será
Comparando
estas coordenadas con las del vector 
, obtenemos la razón de homotecia, de valor k tal que 
. Un sencillo cálculo demuestra la proporcionalidad de los
vectores con razón de semejanza
El centro de
homotecia vendrá dado por el punto de corte de las rectas 
y 
. Si denotamos por 
al centro de homotecia, entonces tenemos que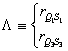 
,
cuyo cálculo es muy fácil de determinar, puesto que tenemos
todo lo disponible. pero sería, sin embargo, extraordinariamente laborioso, y
lo mismo que la razón de semejanza, muy probablemente quedarían sus coordenadas
en función de d y e a partir de nuestro planteamiento de
resolución del problema. Creemos que tal cantidad de trabajo no aporta nada
nuevo. Simplemente se trata de determinar las ecuaciones que pasan por los
puntos 
y 
, cuyas coordenadas ya las tenemos determinadas
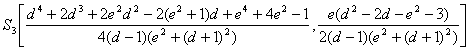
y resolver el sistema correspondiente asociado a ambas líneas
rectas.
(d) Demostremos que se
cumple, y. Basta determinar las coordenadas de los seis vectores.
El vector viene dado por
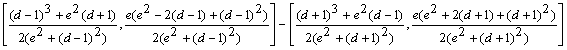
y el vector
por
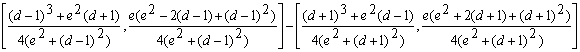
Una simple inspección visual demuestra que .
De forma análoga procedemos para demostrar
que. Tenemos que
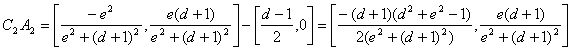
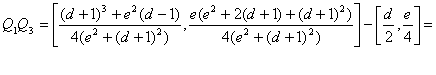
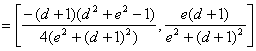con lo que
Finalmente
tenemos que demostrar que. Tenemos que
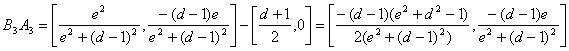
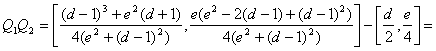
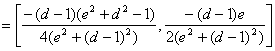con lo que