De investigación

Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)

Problema 449

En el plano de una circunferencia de centro O y radio r, se dan dos puntos cualesquiera A y P. Trazar por P una secante que corta a la circunferencia en B y C de forma que el triángulo ABC sea rectángulo

Sokolowsky, D. (1988): Crux Mathematicorum (32). P1 (p.188)

Honsberger, R. (1996): From Erdös to Kiev (p. 147), con la solución de George Tsintsifas (Tessaloniki, Greece).

( Se pide una solución distinta de las publicadas.)

Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fuenlabrada

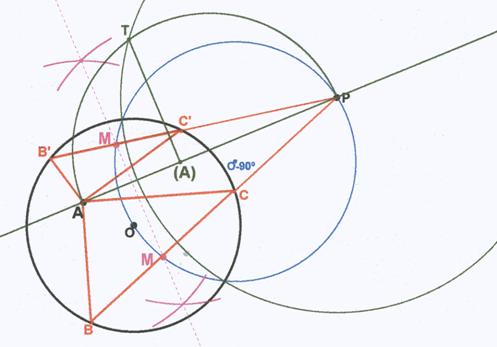
El punto medio M de la hipotenusa BC es la intersección de dos lugares geométricos:

1º.- por ser M el punto medio de la cuerda BC, es el pie de la perpendicular trazada desde el centro de la circunferencia O. Por lo tanto M está en el arco capaz de 90º del segmento OP.

2º.- M es el centro de la circunferencia que pasa por ABC (no dibujada). La potencia del punto P con respecto a la circunferencia dada es la misma que la que tiene a la circunferencia que pasa por los puntos ABC por tener la cuerda BC común. ( PC x PB = PT²). Se trata de obtener el punto (A) de la circunferencia que pasa por ABC (no dibujada) para que se cumpla el producto de la potencia: PA x P(A) = PT². Hallado (A), por el teorema del cateto, el centro M de la circunferencia que pasa por A, B, C y (A) está en la mediatriz de A-(A)