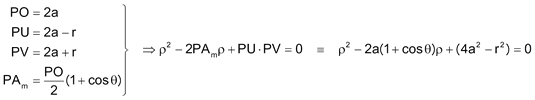|
De investigación. Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)
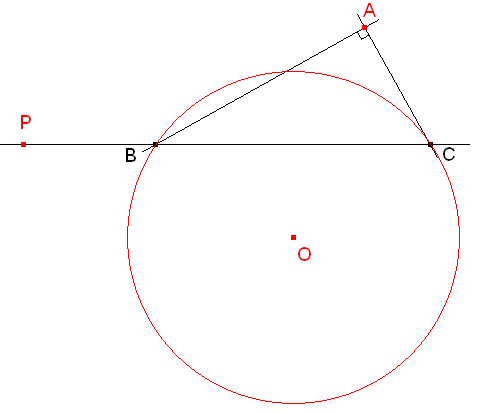
Problema 449 En el plano de una circunferencia de centro O y radio r, se dan dos puntos cualesquiera A y P. Trazar por P una secante que corta a la circunferencia en B y C de forma que el triángulo ABC sea rectángulo.
Sokolowsky, D. (1988): Crux Mathematicorum (32). P1 (p.188) Honsberger, R. (1996): From Erdös to Kiev (p. 147), con la solución de George Tsintsifas (Tessaloniki, Greece).
( Se pide una solución distinta de las publicadas.)
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de marzo de 2008) |
|
INTRODUCCIÓN |
|
Vamos a presentar tres soluciones, una original, la debida a George Tsintsifas y una tercera con lugares geométricos complejos (una cuártica) por medio de CABRI II Plus . En la solución original, estudiaremos la existencia de las soluciones según las distintas posiciones de A respecto de P y del círculo dado.
Para nuestra solución necesitamos recordar que el lugar de los puntos que equidistan de dos puntos dados es una recta (mediatriz), que el ángulo inscrito en un diámetro de la circunferencia es recto y la potencia de un punto respecto a una circunferencia.
Para la solución de George Tsintsifas, además del teorema de Pitágoras, necesitamos recordar que en un triángulo rectángulo el punto medio de la hipotenusa equidista de los vértices
figura 1 y que en cualquier triángulo del que se conoce la mediana
|
|
MI SOLUCIÓN |
|
|
ESTUDIO DE LA FIGURA
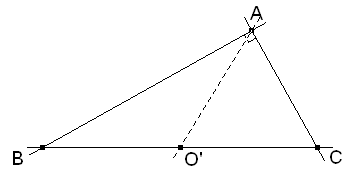
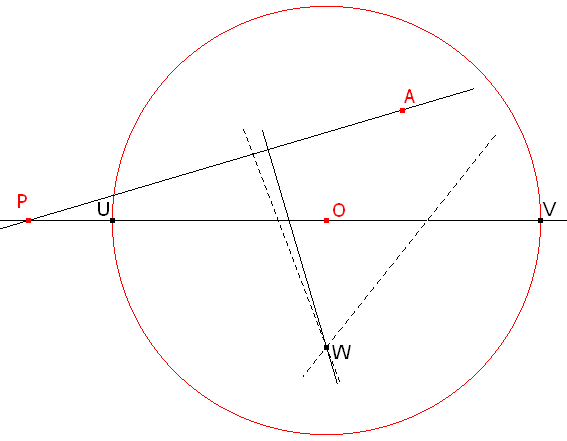
figura 2 Supongamos primero que tenemos el problema resuleto.
figura 3
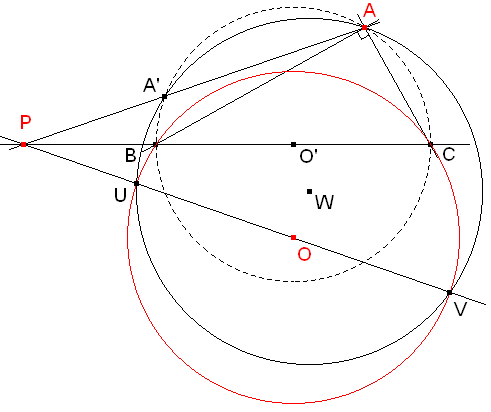
Si BAC es un ángulo recto, está inscrito en un círculo de centro O' del que BC es un diámetro. A' sería el otro punto de intersección de PA con este círculo.
La potencia del punto P respecto a dicho círculo es
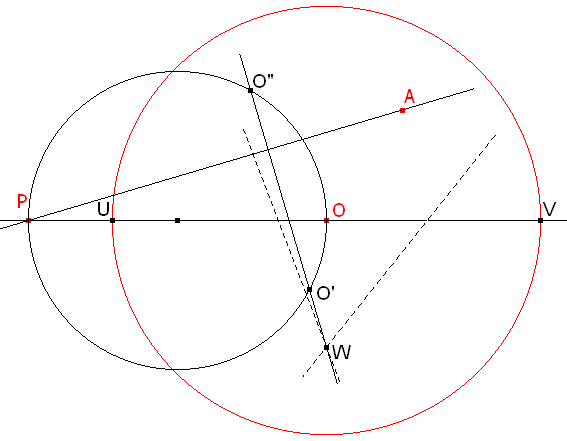
coincide además con la potencia de P respecto al círculo dado de centro O. Por tanto, A, A', U, V están en un mismo círculo de centro W.
figura 4
La mediatriz de A'A pasa por O'. Pero el ángulo PO'O es recto, por lo que O' también se encuentra sobre el círculo de diámetro PO.
Como P y el círculo de centro O son conocidos, podemos hallar U y V. Con las mediatrices de AU y AV hallamos el centro W. No hace falta trazar el círculo ya que A' no es necesario; pues una perpendicular por W a PA es la mediatriz de A'A que corta al círculo de diámetro PO en O'.
La solución nos la da la recta PO'. Como la recta puede tener hasta dos puntos de intersección con el círculo, podemos obtener hasta dos soluciones.
EL MÉTODO DE SOLUCIÓN
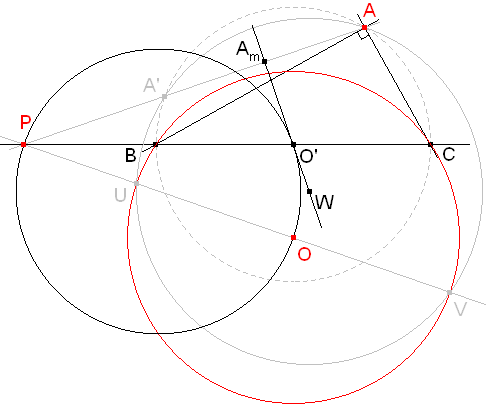
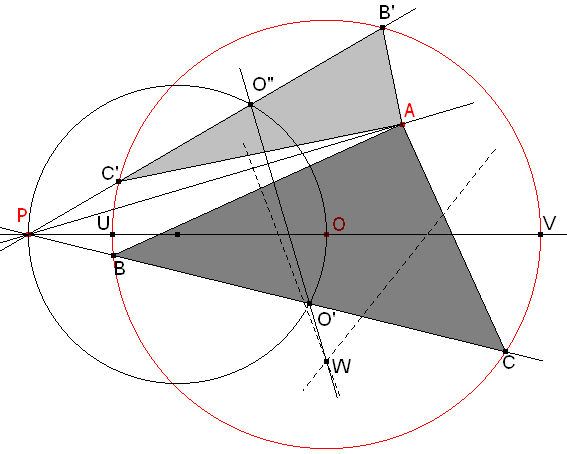
figura 5
Trazamos PO y obtenemos los puntos U y V. Las mediatrices de AU y AV se encuentran en W. Una perpendicular a PA desde W es la mediatriz de A'A.
figura 6
Trazamos el círculo de diámetro PO. Su intersección con la perpendicular anterior, por W, nos proporciona O' y O".
figura 7
La recta PO' corta al círculo dado en B y en C. El triángulo ABC es la solución pedida. La recta PO" nos proporciona la segunda solución.
EXISTENCIA DE SOLUCIONES
Estudiemos parte de la figura 4.
figura 8
Para una dirección cualquiera de PA, si hay solución, existe un punto A' y otro punto Am tales que
Lo que nos indica que PA y PA' son soluciones del polinomio de segundo grado
figura 9
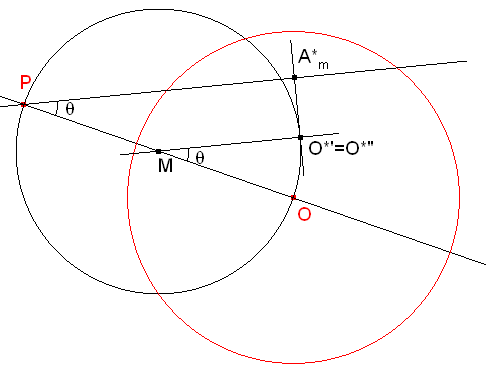
Cuando la mediatriz de A'A sea tangente al círculo de diámetro PO sólo habrá una solución; y a partir de ahí, ninguna. El punto A*m para el que la mediatriz es tangente al círculo lo obtenemos de la siguiente manera. Sea M el centro del círculo de diámetro PO. Por un punto cualquiera O*' sobre el círculo, trazamos la tangente que corta a la paralela a MO*' trazada por P en A*m.
Es fácil ver que la ecuación en polares de A*m, si P es el polo y PO el eje polar, es de la forma
Esta ecuación sustituyendo a PAm en la ecuación anterior de PA nos proporciona el lugar límite para la existencia de soluciones.
y que en cartesianas queda como
Debo agradecer aquí a Francisco Javier García Capitán sus indicaciones para lograr un tratamiento sencillo de estas curvas por medio de software matemático.
Para trazar la curva, podemos además construir un punto A* asociado a A*m y luego pedir a CABRI que nos trace el lugar de A* cuando varíaO*'. Pero existe un método más sencillo
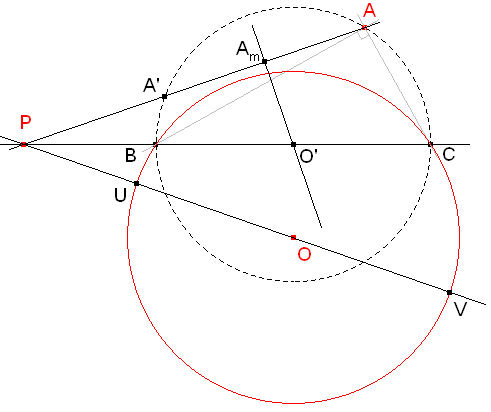
figura 10
Retomamos la figura 4, y tomamos un punto cualquiera O*' sobre el círculo de diámetro PO. Para la la recta PO*', que corta al círculo dado en B* y C*, cualquiera punto A sobre el círculo de diámetro B*C* es solución. Entonces la envolvente de los círculos B*C* cuando variamos O*' nos dará el lugar límite para la existencia de soluciones.
Si le pedimos a CABRI dicho lugar, obtenemos la curva que aparece en azul y cuya ecuación hemos determinado más arriba.
El lugar determinado delimita la zona de existencia de dos soluciones para el punto A. La frontera de esta zona es el lugar de los puntos A para los que la solución es única. Fuera de esa zona no existen soluciones.
Puede apreciarse todo junto en la construcción dinámica que sigue que es la continuación de nuestra construcción de la figura 7.
Puede mover los elementos en rojo
figura 11 Puede mover los elementos en rojo
|
|
LA SOLUCIÓN DE GEORGE TSINTSIFAS |
|
|
ESTUDIO DE LA FIGURA
figura 12
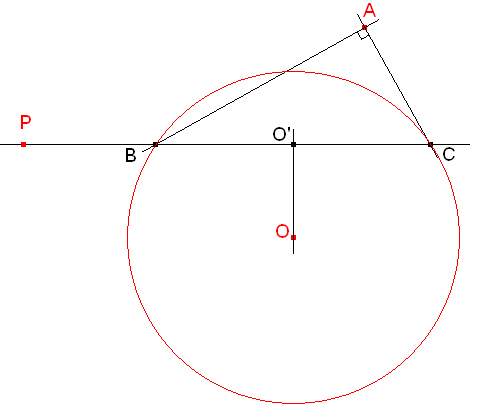
Suponiendo el problema resuelto, tratamos de hallar un punto que nos dé el máximo de información par la construcción buscada. Es claro que si hallamos el punto O' , punto medio de BC, PO' nos da la solución. Además como punto medio de la hipotenusa, goza de la propiedad de equidistar de los vértices del triángulo; y esto le da una ventaja adicional respecto a los demás puntos.
El primer lugar geométrico al que pertence O' es fácil de ver. el ángulo PO'O es recto, y por tanto O' estará sobre la circunferencia de diámetro PO (como ya habíamos visto en la solución anterior). Nos falta sólo una propiedad adicional para el punto O'.
Por el teorema de Pitágoras,
y como O'C=O'A
figura 13
Y recordando el teorema que involucra la mediatriz O'D, D es el punto medio de OA, para el triángulo OO'A, tenemos
que nos lleva a
y despejando obtenemos
Obtenemos que el segundo lugar para O' es la circunferencia de centro D y radio O'D.
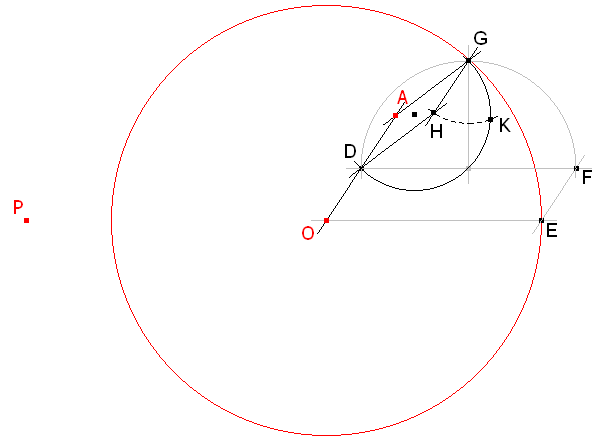
EL MÉTODO DE SOLUCIÓN Haremos la construcción entorno a D, el punto medio de OA.
figura 14
Por O, una recta que corta al círculo dado en E, por D una paralela a OE y por E una paralela a OA que encuentra la paralela anterior en F. Esto nos asegura que DF=OE=r.
Trazamos el semi-círculo de diámetro DF; la mediatriz de DF encuentra al semi-círculo en G. Esto nos asegura que DG2=½r2.
figura 15
Trazamos el semi-círculo de diámetro DG. Por medio de paralelas trazamos GH=½OA. Un arco con centro en G y radio GH corta al último semi-circulo en K. Entonces DKG es un ángulo recto y DO'=DK.
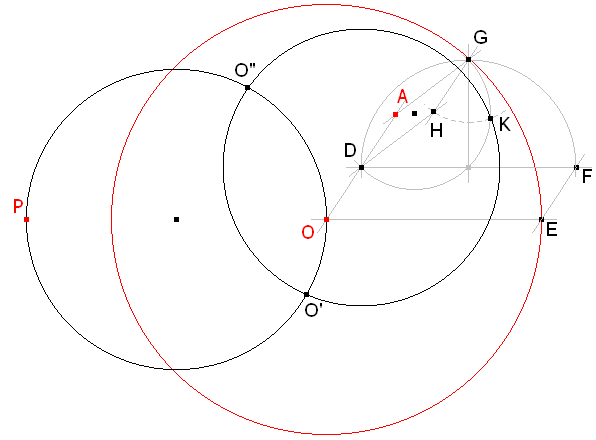
figura 16
El círculo de centro D y radio DK encuentra al círculo de diámetro PO en O'. La segunda intersección O" proporciona una segunda solución.
figura 17
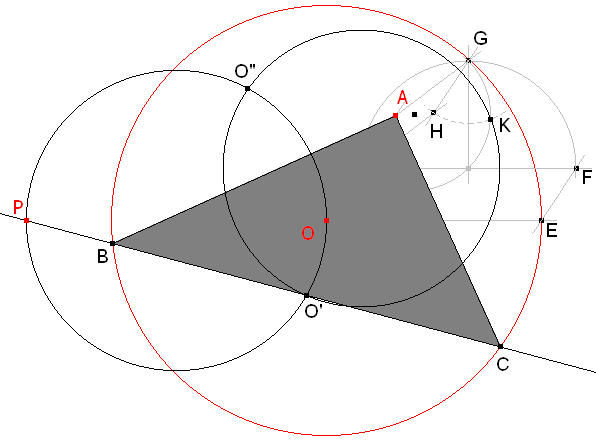
La recta PO' corta al círculo dado en B y en C. El triángulo ABC es la solución pedida.
La recta PO" nos proporciona la segunda solución, tal como se aprecia en la construcción dinámica que sigue.
Puede mover los elementos en rojo
figura 18 Puede mover los elementos en rojo |
|
SOLUCIÓN CABRI |
|
|
figura 19
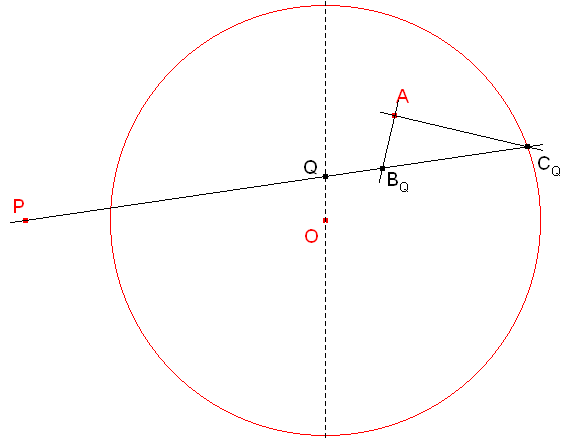
Trazamos una recta auxiliar por el centro del círculo dado. Sobre esta recta, tomamos un punto cualquiera Q. La recta PQ corta al círculo en CQ.
Trazamos ACQ y luego, por A una perpendicular a ACQ. Esta perpendicular corta a PQ en BQ.
Si PQ fuera solución, BQ estaría, además, sobre la circunferencia dada. En general, no es así.
figura 20
Para cada punto Q, hay un punto BQ. Le pedimos a CABRI II Plus, el lugar geométrico de BQ al variar Q sobre su recta.
El lugar geométrico hallado, un cuártica, encuentra al círculo dado en dos puntos B y C'.
La recta PB corta al círculo en otro punto C. El triángulo ABC es la solución podida.
El punto C' nos proporciona la segunda solución, tal como se aprecia en la construcción dinámica que sigue.
Puede mover los elementos en rojo
figura 21 Puede mover los elementos en rojo |