Problema 449

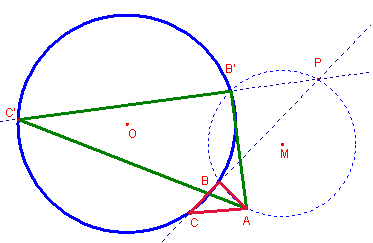En el plano de una circunferencia de centro O y radio r, se dan dos puntos cualesquiera A y P. Trazar por P una secante que corta a la circunferencia en B y C de forma que el triángulo ABC sea rectángulo

Sokolowsky, D. (1988): Crux Mathematicorum (32). P1 (p.188)

Honsberger, R. (1996): From Erdös to Kiev (p. 147), con la solución de George Tsintsifas (Tessaloniki, Greece)

Solución de Ricard Peiró:

Sea .

Sea M el punto medio del segmento

Supongamos resuelto el problema, sean B, C dos puntos de la circunferencia tal que y B; C, P alineados.

Entonces, .

Entonces dibujando la circunferencia de centro M que pasa por el punto A, todos sus puntos Q forman un ángulo .

La intersección de la circunferencia inicial y esta nos da el punto B que buscamos.

Dibujando la recta PB intersecta la circunferencia inicial en el punto C.

El triángulo , .

El problema no tiene solución si .

El problema tiene solución única si .

El problema tiene dos soluciones si .