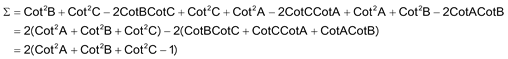De investigación. Propuesto por Vicente Vicario García, I.E.S. “EL SUR”, Huelva. Problema 450. Sea un triángulo ABC, con la notación habitual (Δ=área de ABC):
a) Demostrar la igualdad
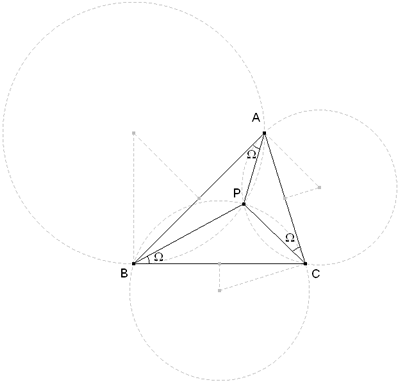
b) Sea P uno de los puntos de Brocard del triángulo ABC, es decir, un punto interior al mismo tal que
donde Ω es el ángulo de Brocard. Admitiendo la existencia del punto P demostrar que Ω≤30°. Vicario, V. (2007): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de marzo de 2008) |
|
SOLUCIÓN |
|
Antes de empezar, indicaremos una construcción fácil de los puntos de Brocard. La definición que se da en el apartado (b) conlleva dos posibilidades:
i ∠APB = π - B, ∠BPC = π - C, ∠CPA = π - A. ii ∠AP’B = π - A, ∠BP’C = π - B, ∠CP’A = π - C. La construcción de la figura es a partir de i. (Ver Trajan Lalesco, La géométrie du triangle, Vuibert, Paris 1952) a) Observando el triángulo APC de la figura deducimos (teorema de los senos)
si dividimos por SenA y desarrollamos
de donde obtenemos la ecuación [1]
Retomando la igualdad inicial
y análogamente
Y sumando las tres últimas igualdades
y añadiendo la ecuación [1]
b) Si elevamos ahora la ecuación [1] al cuadrado, obtenemos la ecuación [2]
Si escribimos la siguiente suma de cuadrados
nos queda
e introduciendo ahora la ecuación [2]
pero Σ, como suma de cuadrados, es no negativa, luego
|

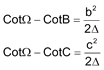
![Eqn10 - Ecuación [2]](sol450ped/Eqn10.gif)