Problema 450

Siga el triangle . Demostreu:

a) .

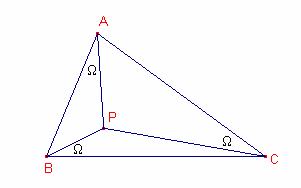
b) Siga P el punt de Brocard del triangle , és a dir, un punt interior al triangle tal que , on s’anomena angle de Brocard.

Demostreu que .

Vicario, V. (2007): Comunicación personal.

Solució Ricard Peiró:

a)

.

Aplicant el teorema del sinus i del cosinus:

.

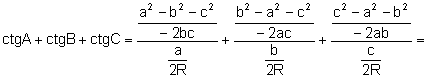
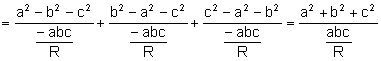L’àrea del triangle és , aleshores:

Aleshores,

.

b)

Si és l’angle de Brocard, aleshores,

. .

Provem l’existència del punt P de Brocard:

Determinem el lloc geomètric del punt tal que .

, aleshores:

.

Aleshores, .

Per tant el lloc geomètric del punt és el conjunt de punts tals que , és constant i independent de , és l’arc capaç construït sobre i angle . Circumferència que passa pels punts A, C i és tangent al costat .

Anàlogament, Determinem el lloc geomètric del punt tal que , és l’arc capaç construït sobre i angle . Circumferència que passa pels punts A, B i és tangent al costat

Si Els punts d’intersecció de les dues circumferències és A i un altre punt únic P.

Provem que .

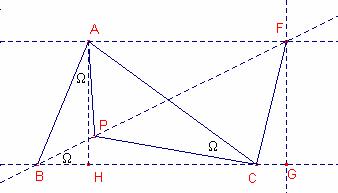
Pel punt A tracem una paral·lela al costat que talla la recta BP en el punt F.

Notem que .

. Per tant, .

Tracem la perpendicular a la recta BC que passa pel punt F que talla aquesta recta en el punt G.

Tracem la perpendicular a la recta BC que passa pel punt A que talla aquesta recta en el punt H.

Notem que .

Per ser , aleshores, el quadrilàter PAFC és inscriptible.

Per tant, , .

Aplicant raons trigonomètriques al triangle rectangle : .

.

Aplicant raons trigonomètriques al triangle rectangle : .

Aplicant raons trigonomètriques al triangle rectangle : .

Aplicant raons trigonomètriques al triangle rectangle : .

.

Vegem que .

Aplicant el teorema dels sinus i la fórmula de l’àrea:

.

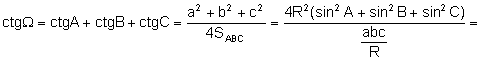
Aplicant la desigualtat de Cauchy-Schwarz:

.

.

Aplicant la desigualtat entre la mitjana aritmètica i geomètrica:

.

.

Aleshores:

Aplicant la desigualtat de Jensen .

.

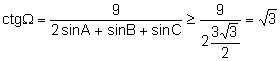La igualtat s’assoleix quan el triangle és equilàter.

.

Com la funció és decreixent:

.