Problema 450

Sea el triángulo . Demostrar:

a) .

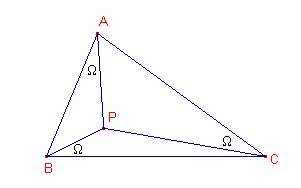
b) Sea P el punto de Brocard del triángulo , es decir, un punto interior al triángulo tal que , donde se llama ángulo de Brocard.

Demostrar que .

Solución Ricard Peiró:

a)

.

Aplicando el teorema de los senos y del coseno:

.

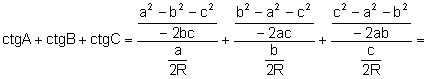
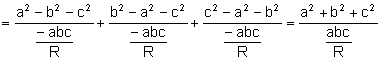El área del triángulo es , entonces:

Entonces,

.

b)

Si es el ángulo de Brocard, entonces,

. .

Probemos la existencia del punto P de Brocard:

Determinemos el lugar geométrico del punto tal que .

, entonces:

.

Entonces, .

Por tanto el lugar geométrico del punto es el conjunto de puntos tales que , es constante y independiente de , es el arco capaz construido sobre y ángulo . Circunferencia que pasa por los puntos A, C y es tangente al lado .

Análogamente, Determinemos el lugar geométrico del punto tal que , es el arco capaz construido sobre y ángulo . Circunferencia que pasa por los puntos A, B y es tangente al lado

Si Los puntos de intersección de las dos circunferencias es A y otro punto único P.

Probemos que .

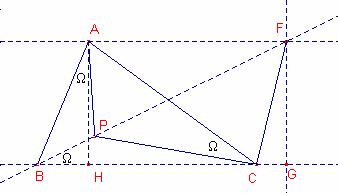
Por el punto A tracemos una paralela al lado que corta la recta BP en el punto F.

Notemos que .

. Por tanto, .

Tracemos la perpendicular a la recta BC que pasa por el punto F que corta esta recta en el punto G.

Tracemos la perpendicular a la recta BC que pasa por el punto A que corta esta recta en el punto H.

Notemos que .

Por ser , entonces, el cuadrilátero PAFC es inscriptible.

Por tanto, , .

Aplicando razones trigonométricas al triángulo rectángulo : .

.

Aplicando razones trigonométricas al triángulo rectángulo : .

Aplicando razones trigonométricas al triángulo rectángulo : .

Aplicando razones trigonométricas al triángulo rectángulo : .

.

Veamos que .

Aplicando el teorema de los senos y la fórmula del área:

.

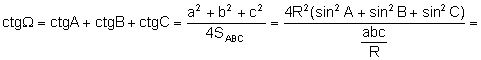
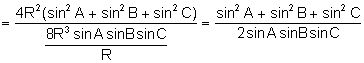Aplicando la desigualdad de Cauchy-Schwarz:

.

.

Aplicando la desigualdad entre la media aritmética i geométrica:

.

.

Entonces:

Aplicando la desigualdad de Jensen .

.

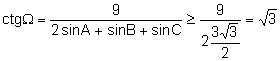La igualdad se alcanza cuando el triángulo es equilátero.

.

Como la función es decreciente:

.