Problema 450.- Sea un triángulo ABC, con la notación habitual (= área de ABC)

(a) Demostrar la igualdad:

(b) Sea P uno de los puntos de Brocard del triángulo ABC, es decir, un punto interior al mismo tal que , donde es el ángulo de Brocard. Admitiendo la existencia del punto P demostrar que .

Vicario, V, (2007): Comunicación personal

Resolución de Vicente Vicario García, I.E.S. “El Sur”, Huelva:

(a) Utilizaremos la notación habitual en la geometría del triángulo. Para demostrar la igualdad propuesta demostramos previamente dos lemas que necesitaremos después.

Lema 1: “En todo triángulo ABC se cumple ”.

Demostración:

.

donde hemos empleado la fórmula de Herón y la fórmula para el área del triángulo junto con la conocida relación .

Lema 2: “En todo triángulo ABC se cumple ”.

Demostración:

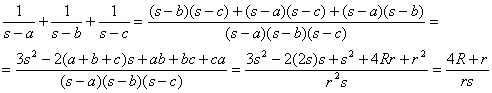
donde hemos vuelto a aplicar la fórmula de Herón y el lema 1.

Utilizaremos ahora algunas relaciones trigonométricas elementales, la expresión para la tangente del ángulo doble en función de la tangente del ángulo simple, la relación y análogas, los lemas 1 y 2 junto con manipulaciones algebraicas: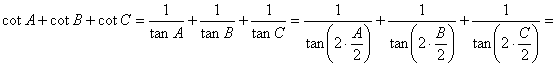

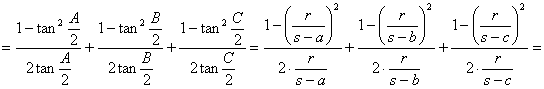
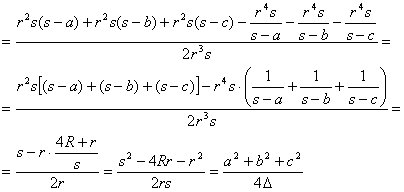
ya que tenemos

(b) Considerando a P como un punto interior y usando las caracterizaciones definidas sobre dicho punto tenemos claramente que

[1]

Aplicando el teorema de los cosenos a los triángulos PAB, PBC y PCA tenemos que

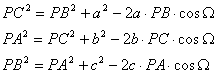[2]

y sumando miembro a miembro las expresiones de [2] entonces

y utilizando [1], tenemos

Finalmente, para obtener la desigualdad , planteamos la desigualdad equivalente . Esta última desigualdad es la famosa desigualdad de Weitzenböck, que admite multitud de demostraciones alternativas. Una demostración sencilla y elegante es la siguiente:

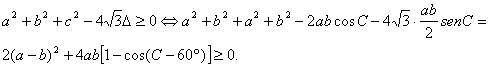
donde hemos aplicado el teorema de los cosenos y relaciones trigonométricas básicas junto con la expresión para el área del triángulo.

---oooOooo---