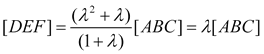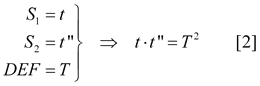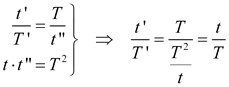|
De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid. Problema 451. Sean dos triángulos ABC y A´B´C´ y construimos los triángulos DEF y D´E´F´, circunscritos respectivamente a ABC y A´B´C´, y tales que los lados de DEF (D´E´F´) sean paralelos a los lados respectivos de A´B´C´(ABC). Si designamos por t, t´, T, T´ las áreas de ABC, A´B´C´, DEF, D´E´F´, demostrar que t/t´=T/T´. Sur les triangles isncrits dans un triangle donné, A propos d'un article de M.E. Feldheim, en la revista L´Enseignement mathématique, (t. 37, 329-335, 1938) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de abril de 2008) |
|
SOLUCIÓN |
|
|
Puede encontrarse el original y una solución de este enunciado en Felheim - L’Enseignement mathématique, (t. 37, 329-335, 1938) La solución allí presentada es trigonométrica, nosotros haremos una por homotecias y usaremos un teorema sobre la media geométrica de las áreas de dos triángulos (inscrito e inscrito) para el que se puede consultar la fuente original.
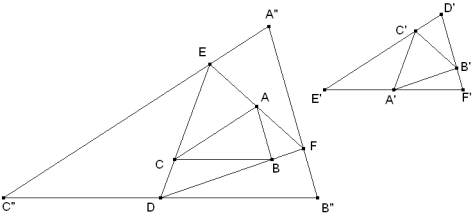
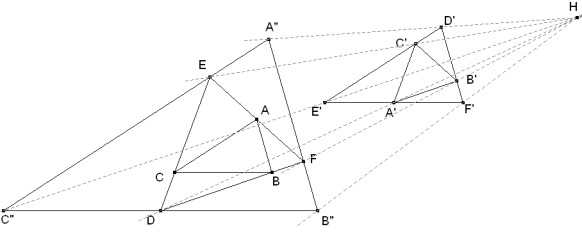
Dibujamos el enunciado; pero en lugar de usar esta figura, seguimos repitiendo la construcción trazando un triángulo A"B"C" circunscrito a DEF y de lados paralelos a ABC.
Por tener los lados paralelos, el triángulo A"B"C" es homotético a D'F'E' y el triángulo EDF es homotético a C'A'B' en la misma homotecia anterior ya que A"B"C" está circunscrito a EDF y D'E'F' está circunscrito a A'B'C'. Si ρ es la razón de esa homotecia de centro H (ver figura), ρ² es la razón de áreas de las figuras homotéticas. En esas condiciones se cumple
Introduciendo la nomenclatura del enunciado llamando t" al área de A"B"C" nos queda
TEOREMA
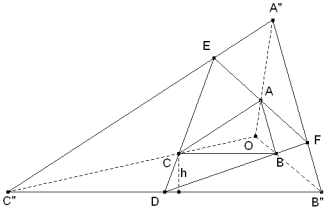
Como los triángulos A"B"C" y EDF tienen los lados paralelos son homotéticos en una homotecia de centro O (ver figura) y razón λ. Si consideramos, por ejemplo, los triángulos B"OC" y BOC tenemos
Ahora vinculamos el área del trapecio B"C"CB y el área del triángulo BCD
y análogamente para el resto de trapecios y nos queda
y sumando las tres ecuaciones miembro a miembro
Que nos permite expresar [DEF] en función de [ABC]
De donde
que nos proporciona la prueba del teorema. Si introducimos la notación del enunciado en el teorema anterior
Combinando ahora los resultados [1] y [2]
que es el resultado que solicita el enunciado. |
![Eq 02 = [1]](sol451ped/Eqn2.gif)
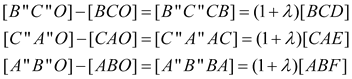
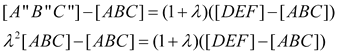 .
.