De investigación
Propuesto
por Juan Bosco Romero Márquez, profesor colaborador de
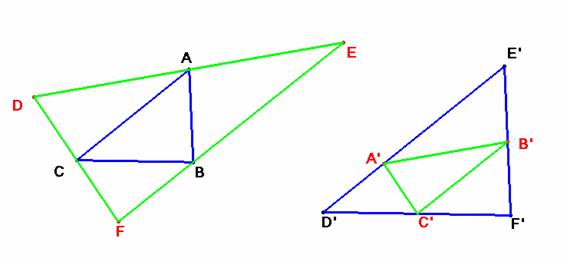
Problema 451.- Sean dos triángulos ABC y A´B´C´ y construimos los triángulos DEF y D´E´F´, circunscritos respectivamente a ABC y A´B´C´, y tales que los lados de DEF (D´E´F´)
sean paralelos a los lados respectivos de A´B´C´(ABC). Si designamos
por t, t´, T, T´ las
áreas de ABC, A´B´C´, DEF, D´E´F´,
demostrar que t/t´ = T/T´.
Sur
les triangles isncrits dans un triangle donné, A propos d'un article de M.E.
Feldhein, en la revista ´Enseignement mathématique, (t. 37, 329-335, 1938)
Solución de Saturnino Campo Ruiz. profesor del IES Fray Luis de León, de Salamanca (7 de abril de 2008)
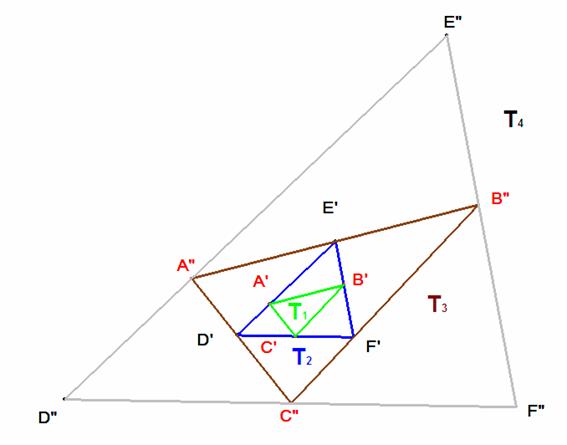
Según un problema anterior (nº 162), sabemos que si se tienen tres triángulos cada uno inscrito en el siguiente, tales que el primero y el último tienen sus lados paralelos, las áreas de estos triángulos están en progresión geométrica, siendo la razón de la misma igual a la de semejanza del primer triángulo y el tercero. Si seguimos inscribiendo triángulos indefinidamente se obtiene una sucesión de triángulos cuyas áreas forman una progresión geométrica.
Llamando S1, S2, S3, S4, … , Sn … a las áreas de estos triángulos y considerando los tres primeros se tiene: S2 = k·S1 y S3= k2·S1, siendo k la razón de semejanza de T1 y T3.
Tomando el segundo, el tercero y el cuarto, S3 =h·S2=h·kS1 y S4 =h2·S2= h2·kS1 y h es la razón de T2 y T4.
Igualando las dos expresiones del área del tercer triángulo tenemos h·kS1 = k2·S1, de donde se deduce que h y k son iguales.
En resumen, lo que obtenemos es que en una sucesión de triángulos como la descrita, la razón de las áreas de dos consecutivos es constante e igual a la razón de semejanza. La razón de semejanza de los que ocupan el lugar impar es, por tanto, igual a la de los triángulos que ocupan lugar par.
Para la primera figura tenemos [DEF]=k[ABC] y en la segunda [D’E’F’]=k[A’B’C’]. El cociente de ambas expresiones es la igualdad que queríamos
demostrar. ![]()