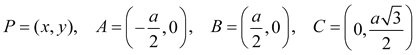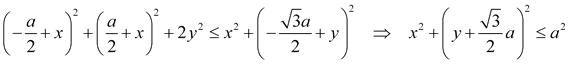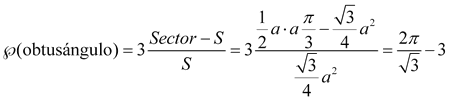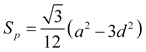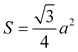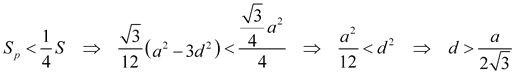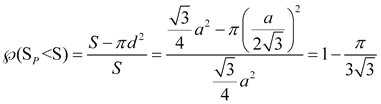Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva

Problema 453.- Sea un triángulo equilátero ABC. Se escoge al azar un punto P en su interior. Hallar la probabilidad de que el triángulo de Pompeïu de lados PA, PB, PC, así formado:

(a)       Sea obtusángulo

(b)       Tenga área menor que la cuarta parte del área del triángulo equilátero original.

Vicario, V. (2008): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de abril de 2008)

SOLUCIÓN

(a)

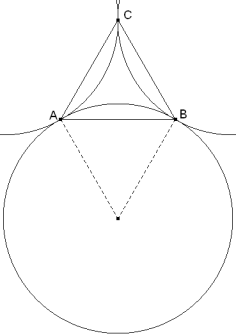
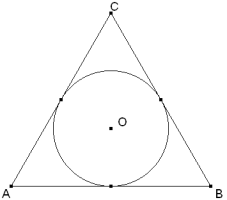
Para que el triángulo de Pompeïu sea obtusángulo, basta que esté en el interior de cualquiera de los tres círculos de radio a y centro en el punto simétrico respecto al lado del vértice opuesto a ese lado.

Para verlo, imaginemos un sistema de coordenadas con eje de abscisas AB y eje de ordenadas la altura por C.

Los lados del triángulo de Pompeïu son PA, PB, PC y el triángulo será obtusángulo en el momento que deje de ser recto. Por lo tanto, apoyándonos en el teorema de Pitágoras, se deberán cumplir tres condiciones de la forma

...

Si el lado del triángulo equilátero es a, suponemos

Por lo tanto la condición anterior queda como

Es decir, P debe ser interior al triángulo equilátero y al círculo de radio a y centro el punto simétrico de C respecto al lado AB. Análogamente para los círculos de los otros dos lados.

Para calcular el área del círculo interior al triángulo basta ver que el ángulo AC'B es de ⅓π y por lo tanto el área será el área del sector circular menos el área del triángulo que coincide con el área del triángulo original (a trazos en la figura). Con lo que la proporción de áreas (teniendo en cuenta que hay tres círculos posibles) queda como

(b)

En la solución del problema 424 obtuvimos el área del triángulo de Pompeïu

donde a es el lado del triángulo equilátero y d es la distancia entre P y O (el centro del círculo circunscrito que en el triángulo equilátero coincide con el baricentro, el ortocentro y el centro del círculo inscrito). Sabemos también el área del triángulo equilátero de lado a

La condición del apartado es

de donde d ha de ser mayor que el radio del círculo inscrito (en el triángulo equilátero, un tercio de la altura); en consecuencia P debe ser interior al triángulo equilátero y exterior a su circo inscrito. La proporción de áreas queda como