Problema 1.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva)

Sea un triángulo equilátero ABC. Se escoge al azar un punto P en su interior. Hallar la probabilidad de que el triángulo de Pompeiu de lados PA, PB, PC, así formado:

(a) Sea obtusángulo

(b) Tenga área menor que la cuarta parte del área del triángulo equilátero original

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

(a) Sea L la longitud del lado del triángulo equilátero ABC. Sabemos que si P es un punto interior al triángulo equilátero, el triángulo de Pompeiu de lados PA, PB y PC, puede ser explícitamente construido. Consideremos el punto P interior y giremos alrededor del vértice A el triángulo ABP, un ángulo de 60º en sentido contrario a las agujas del reloj. Sea B´ la imagen del vértice B respecto de este giro. Entonces el triángulo CPB´ es el triángulo de Pompeiu, puesto que claramente , y .

Por otra parte, es evidente que , ,

y en consecuencia:

y como , entonces tenemos que

.

Por tanto, si el triángulo de Pompeiu CPB´ es obtusángulo, al menos uno de los ángulos , , ha de ser . Para determinar la probabilidad pedida consideremos el arco capaz interior al triángulo equilátero de 150º relativo a cada lado del mismo, por ejemplo, el del lado BC, y sean D el punto central de dicho arco capaz interior y O, el centro del mismo, (exterior al triángulo). Obviamente, el triángulo OCD es isósceles ya que y además , , . También tenemos que

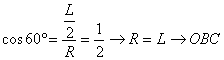es equilátero

Determinemos ahora el área del segmento circular CDB que será el área del sector circular OBC menos el área del triángulo equilátero OBC. Un fácil cálculo proporciona

Área del sector circular CDB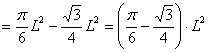

La ecuación de la circunferencia que corresponde al arco capaz BC, tomando ejes coordenados en el vértice B con eje de abscisas sobre el lado BC, es claramente

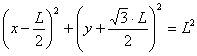
y un sencillo ejercicio de cálculo demuestra que la pendiente de la recta tangente a esta curva en el origen corresponde a un a un ángulo de 30º, ya que

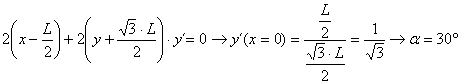
con lo que los arcos capaces considerados en el triángulo equilátero no se superponen. Por tanto, teniendo en cuenta dichos arcos, la probabilidad pedida será

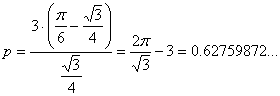
(b) Determinaremos ahora el área del triángulo de Pompeiu de forma distinta a la que aparece en el artículo de József Sándor (FG-2005) y el conocido teorema que ya apareció como problema en esta revista.

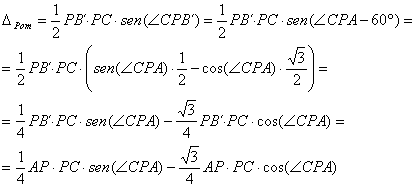
De forma análoga podemos expresar el área del triángulo de Pompeiu tomando otros dos lados del mismo y el ángulo comprendido, de forma que tenemos las siguientes tres expresiones para el área

[1]

[2]

[3]

Teniendo en cuenta que según el teorema de los cosenos aplicado al triángulo APC tenemos y análogamente para los triángulos APB y PBC, sumando las expresiones [1],[2] y [3], entonces

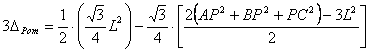
y como se tiene 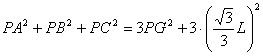, donde G es el baricentro del triángulo equilátero, llegamos a

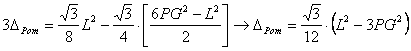[4]

Se puede observar a partir de la expresión [4] que , luego la probabilidad pedida está bien definida. Además se debe tener que

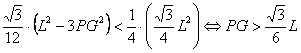
Observemos también que siendo r el radio de la circunferencia inscrita al triángulo equilátero de partida ABC, tenemos fácilmente , luego los puntos que debemos considerar, favorables a nuestro suceso, son los que son exteriores al círculo circunscrito e interiores al triángulo ABC. Entonces, la probabilidad pedida será

---oooOooo---