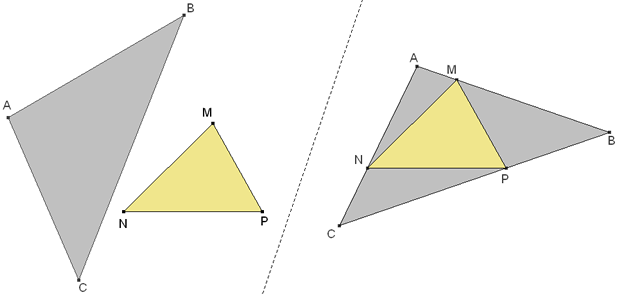
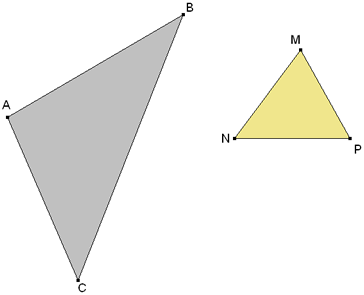
Propuesta de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (noviembre de 2007). Problema 454



MÉTODO DEL PROBLEMA CONTRARIO


“Como vimos en el número 400 extra APOLONIO, HALLEY, NEWTON, PETERSEN, SAPIÑA, RITT, ROSILLO - LA SEMEJANZA”, el problema, que nos ocupa, fue propuesto y resuelto por NEWTON en la sección V del primer libro de su obra:


PHILOSOPHIÆ NATURALIS PRINCIPIA MATHEMATICA


Lemma XXVI


Trianguli fpecie & magnitudine dati tres angulos ad rectas totidem pofitione datas, quæ non funt omnes parallelæ, fingulos ad fingulas ponere.


LemaXXVI


Situar uno a uno los tres ángulos de un triángulo de especie y magnitud dadas sobre tres rectas dadas también en posición y que no sean entre sí paralelas ninguna.


Julius Petersen, con el número 377, también lo incluye en su obra


“Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880)”


Un enunciado actual sería


En un triángulo dado ABC, inscribir otro triángulo congruente a un triángulo dado MNP.


Y como vimos varias soluciones del mismo, proponemos su resolución por un método diferente a los presentados, el método del problema contrario. En lugar de inscribir el triángulo dado MNP en el ABC, procedamos de modo contrario, es decir


CIRCUNSCRIBIR A UN TRIÁNGULO DADO MNP UN TRIÁNGULO CONGRUENTE CON OTRO TRIÁNGULO DADO ABC.

Pedret, J.M. (2007): Comunicación personal


Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de abril de 2008)

 

INTRODUCCIÓN

 

Para poder establecer la solución a este enunciado, suponemos el problema resuelto.


Veremos que la solución se basa en dos construcciones básicas.


A continuación, demostramos los teoremas seis y siete de los que se desprenden directamente las dos construcciones a realizar; pero previamente enunciaremos, sin demostración, los teoremas uno, dos, tres, cuatro y cinco, necesarios para establecer los teoremas seis y siete.


Establecemos la metodología para realizar las construcciones propuestas. La segunda construcción nos proporciona la posibilidad de dos soluciones.


Finalizamos con las dos soluciones posibles al enunciado que pueden extenderse hasta seis.

 

ANÁLISIS DEL PROBLEMA

 

SUPONEMOS EL PROBLEMA RESUELTO


01.png
figura 1


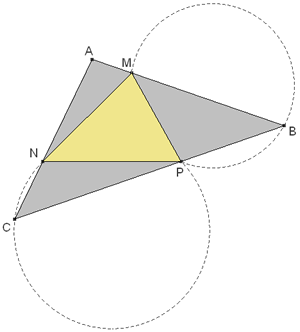
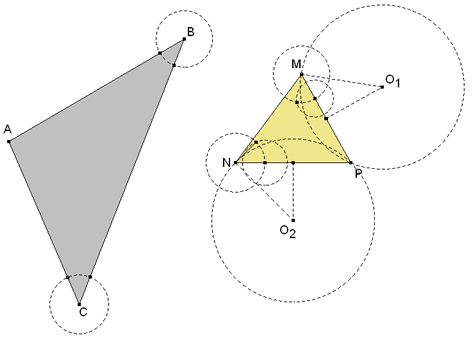
Desde el vértice C, se ve el lado MP bajo un ángulo ∠MCP y que desde el vértice B se ve el lado NP bajo un ángulo ∠NBP.


02.png
figura 2


Sabemos que el lugar de los puntos desde donde se ve un segmento bajo un ángulo dado es el arco capaz de ese ángulo.


Si trazamos el arco capaz del ángulo ∠NCP para el segmento NP y el arco capaz de ángulo ∠MBP para el segmento MP, observamos que el lado BC del triángulo circunscrito tiene un extremo en cada arco capaz, C en el arco de NP y B en el arco de MP; pero además conocemos la longitud del lado BC; entonces nuestro problema se reduce a la aplicación de las siguientes construcciones:


  1. Trazar el aco capaz de un ángulo inscrito en un segmento dado.


  2. Trazar por un punto de intersección de dos circunferencias una recta tal que el segmento comprendido entre las dos circunferencias sea de longitud dada.

 

TEOREMAS SIN DEMOSTRACIÓN

 

TEOREMA UNO

03.png
figura 3


En cualquier triángulo, la suma de sus tres ángulos es igual a dos ángulos rectos.


ESCOLIO UNO


En todo triángulo ABC el ángulo exterior BAD es igual a la suma de dos interiores opuestos B y C; al ser AE paralela a BC, la parte BAE es igual al ángulo B, y la otra parte DAE es igual al ángulo C.


TEOREMA DOS

04.png
figura 4


Si desde un punto A, situado fuera de una recta DE, se lleva la perpendicular AB a esta recta, y diferentes oblicuas AE, AC, AD, ... a diferentes puntos de esa recta:


  1. La perpendicular AB es más corta que cualquier oblicua.


  2. Las dos oblicuas AC, AE trazadas a cada lado de la perpendicular a distancias iguales BC, BE son iguales.


  3. e dos oblicuas cualesquiera AC y AD, o AE y AD, la que más se aleje de la perpendicular será la más larga.

TEOREMA TRES

05.png
figura 5


Si por el medio O de la recta AB, se levanta la perpendicular EF sobre esta recta:


  1. Cada punto de la perpendicular es equidistante de los extremos de la recta A, B.


  2. Todo punto fuera de la perpendicular estará a distancias distintas de los extremos A y B.


TEOREMA CUATRO


En un mismo círculo o en círculos iguales, los arcos iguales subtienden cuerdas iguales, y recíprocamente las cuerdas iguales subtienden arcos iguales.


TEOREMA CINCO


En un círculo, el ángulo formado por la tangente y el radio en el punto de contacto es recto.

 

TEOREMAS CON DEMOSTRACIÓN

 

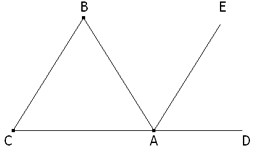
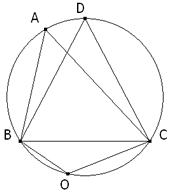
TEOREMA SEIS

06.png
figura 6


Un ángulo BAD inscrito en un círculo tiene por medida la mitad del arco BD comprendido entre sus lados.


Para demostrarlo, probaremos que el ángulo inscrito BAD es la mitad del ángulo en el centro BCD.


Suponemos primero que el centro del círculo está dentro del ángulo BAD, trazamos el diámetro AE y los radios CB, CD. El ángulo BCE, exterior al triángulo ABC, es igual a la suma de los interiores CAB, ABC (TEOREMA UNO): pero el triángulo BAC es isósceles, el ángulo CAB es igual al ABC; entonces el ángulo BCE es el doble de BAC. El ángulo BCE, como ángulo en el centro, tiene por medida el arco BE; luego el ángulo BAC tiene por medida la mitad de BE. Por una razón parecida, el ángulo CAD tiene por medida la mitad de ED: luego BAC+CAD o BAD tiene por medida la mitad de BE+ED o la mitad de BD.


Suponemos, en segundo lugar, que el centro C está situado fuera del ángulo BAD; entonces trazamos el diámetro AE y el ángulo BAE tiene por medida la mitad de BE, el ángulo DAE la mitad de DE; luego su diferencia BAD tiene por medida la mitad de BE menos la mitad de ED, o la mitad de BD.


07.png
figura 7



COROLARIOS SEIS


Todos los ángulos BAC, BDC,... inscritos en el mismo segmento son iguales.

Ya que tienen por medida la mitad del mismo arco y son la mitad del mismo ángulo central.


Así, el arco BAC es el lugar geométrico de los vértices de los triángulos con la misma base BC y con el mismo ángulo en el vértice opuesto a la base.


Podemos decir también que el arco BAC es el lugar de los puntos desde donde se ve el segmento BC bajo un mismo ángulo.


El arco BAC también recibe el nombre de arco capaz del ángulo A inscrito en el segmento BC.


Si BC es un diámetro, el ángulo A es recto, pues es la mitad de la semicircunferencia.


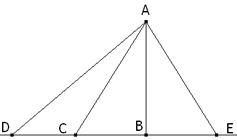
TEOREMA SIETE

08.png
figura 8


“... El radio CG, perpendicular a una cuerda AB, divide a esta cuerda y al arco que subtiende AGB, cada uno en dos partes iguales ...”

Tracemos los radios CA y CB; estos radios son, respecto a la perpendicular CD, dos oblicuas iguales que están igualmente alejadas de la perpendicular (TEOREMA DOS); AD=DB.


Ya que AD=DB, CG es una perpendicular por el punto medio de AB; ya que todo punto de esta perpendicular debe estar a igual distancia de los dos extremos A y B (TEOREMA TRES), el punto G es uno de tales puntos y AG=BG.


Pero si la cuerda AG es igual a la cuerda GB, el arco AG es igual a la al arco GB (TEOREMA CUATRO); y entonces el radio CG, perpendicular a la cuerda AB, divide, por el punto G, al arco que subtiende esta cuerda en dos partes iguales.



ESCOLIO SIETE


La perpendicular levantada por el punto medio de una cuerda pasa por el centro del círculo y por el medio del arco que subtiende la cuerda.

 

PRIMERA CONSTRUCCIÓN

 

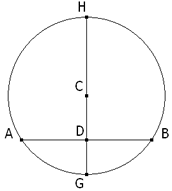
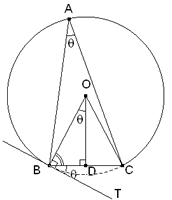
TRAZAR EL ACO CAPAZ DE UN ÁNGULO INSCRITO EN UN SEGMENTO DADO.


Supongamos que tenemos la construcción resuelta.

09.png
figura 9


Si trazamos la tangente por un extremo B del segmento, el ángulo del radio y la tangente es recto (TEOREMA CINCO), OBT es recto. Pero OBT=OBD+DBT de lo que deducimos DBT=OBT-OBD. Por otra parte, en el triángulo rectángulo ODB la suma de sus ángulos es dos rectos (TEOREMA UNO), en consecuencia DOB+OBD vale un ángulo recto y así obtenemos la siguiente igualdad DBT=(DOB+OBD)-OBD=DOB; pero DOB es igual al ángulo inscrito en el segmento (TEOREMA SEIS); por lo que deducimos que deducimos que:


El ángulo entre la tangente al arco capaz por un extremo del segmento dado y el propio segmento es igual al ángulo inscrito.

Este resultado nos proporciona la construcción buscada:


  1. Por un extremo del segmento dado trazamos una recta que forme con ese segmento el ángulo dado.


  2. El centro del círculo que contiene al arco se halla en la mediatriz del segmento (TEOREMA SIETE) y en la perpendicular (el radio) a la recta trazada por el extremo del segmento (TEOREMA CINCO).

 

SEGUNDA CONSTRUCCIÓN

 

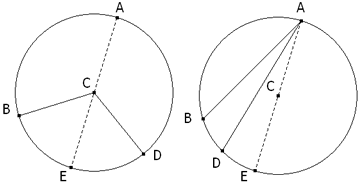
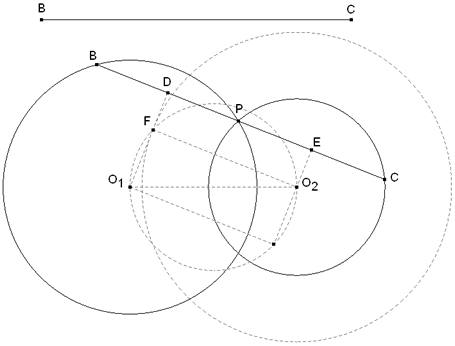
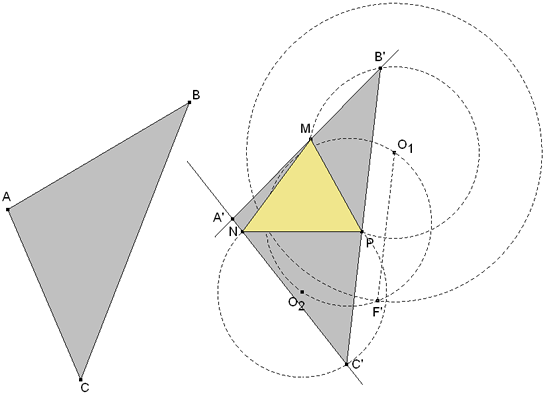
TRAZAR POR UN PUNTO DE INTERSECCIÓN DE DOS CIRCUNFERENCIAS UNA RECTA TAL QUE LA PARTE COMPRENDIDA ENTRE LAS DOS CIRCUNFERENCIAS SEA DE LONGITUD DADA.


De nuevo, suponemos que tenemos la construcción resuelta; siendo el segmento BC la longitud dada, O1 y O2 las circunferencias dadas y P uno de sus puntos de intersección.


10.png
figura 10


El segmento BC determina sendas cuerdas BP y PC en los círculos dados. D y E son los puntos medios respectivos de esas cuerdas. La perpendicular a BP por D pasa por el centro O1 (TEOREMA SIETE), igualmente una perpendicular por E a PC pasa por O2. Una paralela a BC por uno de los centros, por ejemplo O2, corta a la perpendicular O1D en F; con lo que el ángulo O1FO2 es recto. O1FO2 está inscrito en un semicírculo de diámetro O1O2 (TEOREMA SEIS); Y O2F=DE=½BC.


De lo anterior se desprende la siguiente construcción:


  1. Trazamos el círculo de diámetro O1O2.


  2. Con centro en O2 trazamos el círculo de radio ½BC que corta al círculo anterior en F.


  3. Una paralela a O2F por el punto de intersección P nos da la solución.

Observemos que si BC>2O1O2 no hay solución, que el valor máximo de BC es 2O1O2 siendo BC paralelo a O1O2.


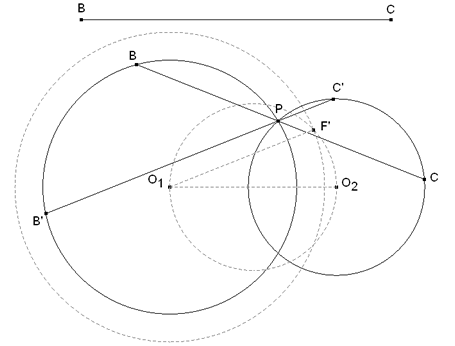
11.png
figura 11


Si trazamos el círculo de centro O1 y radio ½BC, obtenemos el punto F’ de intersección con el círculo de diámetro O1O2. Esto supone que trazando una paralela a O1F que pase por P obtenemos una nueva manera de inscribir el segmento BC, que pasa por P, entre los dos círculos dados. Distinguimos este segmento como B’C’.

 

SOLUCIÓN

 

12.png
figura 12


Sea ABC el triángulo que hay que circunscribir al triángulo dado MNP. Y recordando la figura 2,


13.png
figura 13


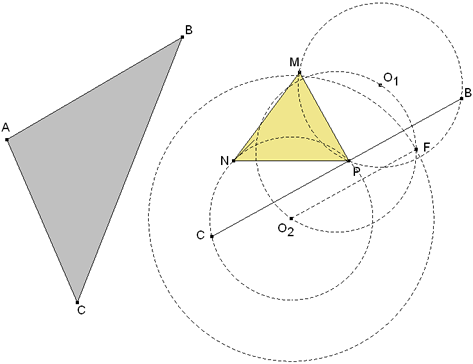
En el triángulo dado ABC medimos el ángulo C y con la PRIMERA CONSTRUCCIÓN trazamos sobre NP el arco capaz de ángulo C. Análogamente, sobre MP, trazamos el arco capaz de ángulo B. P es un punto de intersección de los dos arcos y es el punto por donde pasará el lado del triángulo circunscrito de longitud BC (ver figura 2).



PRIMERA SOLUCIÓN

14.png
figura 14


Mediante la SEGUNDA CONSTRUCCIÓN, con el centro O2, inscribimos el lado de longitud BC entre los dos círculos hallados.


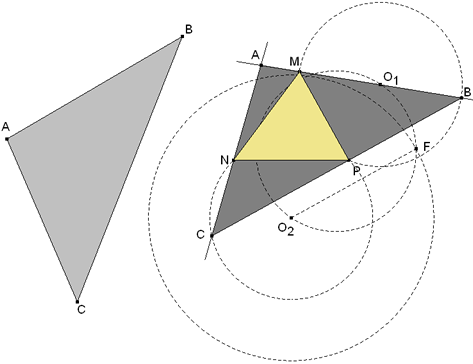
15.png
figura 15


Obtenidos B y C, una recta por B, M y otra recta por C, N se encuentran en el vértice A.



SEGUNDA SOLUCIÓN

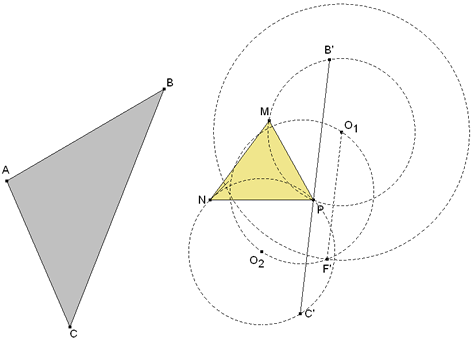
16.png
figura 16


Mediante la SEGUNDA CONSTRUCCIÓN, con el centro O1, inscribimos el lado de longitud BC entre los dos círculos hallados.


17.png
figura 17


Obtenidos B’ y C’, una recta por B’, M y otra recta por C’, N se encuentran en el vértice A’. Veamos en la figura dinámica las dos soluciones simultáneamente.


PUEDE MOVER LOS ELEMENTOS EN ROJO


figura 18

PUEDE MOVER LOS ELEMENTOS EN ROJO


 

OTRAS CUATRO SOLUCIONES

 

En lugar de trazar sobre NP el arco capaz del ángulo C, podemos trazar el arco capaz del ángulo B; entonces trazaríamos por MP el arco capaz del ángulo A e inscribiendo el segmento AB, que pasa por P, entre los dos círculos hallados, obtenemos otras dos soluciones.


También podemos trazar sobre NP el arco capaz del ángulo A y sobre MP el arco capaz de ángulo C con lo que obtendríamos dos soluciones más.


En general, dados dos triángulos, podemos obtener hasta seis soluciones distintas al problema propuesto.