Propuesta de José María Pedret,
Ingeniero Naval. Esplugues de Llobregat
(Barcelona). (noviembre de 2007)
Problema 454
MÉTODO DEL PROBLEMA CONTRARIO
“Como vimos en el número 400 extra ”APOLONIO, HALLEY, NEWTON, PETERSEN, SAPIÑA, RITT, ROSILLO...”, el problema, que nos ocupa, fue propuesto y resuelto por NEWTON en la sección V del primer libro de su obra: PHILOSOPHIÆ NATURALIS PRINCIPIA MATHEMATICA Lemma XXVI Trianguli fpecie & magnitudine dati tres angulos ad rectas totidem pofitione datas, quæ non funt omnes parallelæ, fingulos ad fingulas ponere. LemaXXVI Situar uno a uno los tres ángulos de un triángulo de especie y magnitud
dadas sobre tres rectas dadas también en posición y que no sean entre sí
paralelas ninguna. Julius Petersen, con el número 377, también lo incluye en su obra Un enunciado más actual sería En un triángulo dado ABC, inscribir otro triángulo congruente a un triángulo dado MNP. Y como vimos varias soluciones del mismo, proponemos su resolución por un método diferente a los presentados, el método del problema contrario. En lugar de inscribir el triángulo dado MNP en el ABC, procedamos de modo contrario, es decir Circunscribir a un triángulo dado MNP un
triángulo congruente con otro triángulo dado ABC. |
Pedret, J.M. (2007): Comunicación personal
Solución (salvo una parte de c) de Saturnino Campo Ruiz. profesor del IES Fray Luis de León, de Salamanca (7 de abril de 2008)
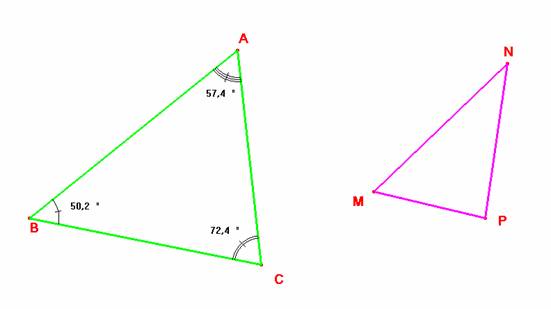
Lo primero que hacemos es trazar por los vértices de MNP paralelas a los lados de ABC. Se consigue así un triángulo circunscrito A’B’C’, semejante a ABC, pero que no es congruente con él en general. Si deseamos construir otro triángulo circunscrito, bastará con observar que los vértices de A’B’C’ están sobre los arcos capaces de los segmentos MP, NP y MN y amplitudes los ángulos A, B y C respectivamente. Eligiendo un vértice C* los otros dos quedan unívocamente determinados.
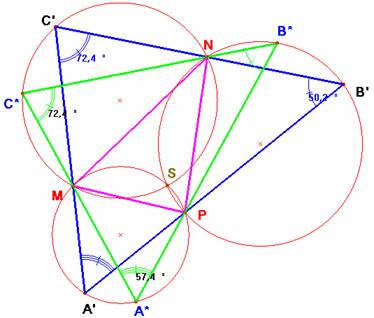
Los triángulos A’B’C’ y A*B*C* son semejantes. En la figura observamos que las circunferencias que contienen los arcos capaces utilizados en la construcción de A*B*C* se cortan en un punto S. Éste es el centro de semejanza. Veámoslo.
Si el segmento A’B’ es homólogo en la semejanza al segmento A*B*, los puntos A’, A* y el punto de intersección P están en una misma circunferencia. Análogamente ocurre con los puntos B’, B* y P.
Estas circunferencias son los
arcos capaces de MP y NP respectivamente. E igualmente con
otro par de lados homólogos. La conclusión obtenida es que TODOS los triángulos circunscritos al triángulo MNP y que son semejantes al ABC tienen un centro común de semejanza:
el punto S.
Para
seleccionar aquél que sea congruente a ABC,
siguiendo la línea de las explicaciones de José María Pedret,
construiremos un triángulo homotético (con centro de
homotecia el de semejanza) a A’B’C’ y que sea congruente con ABC.
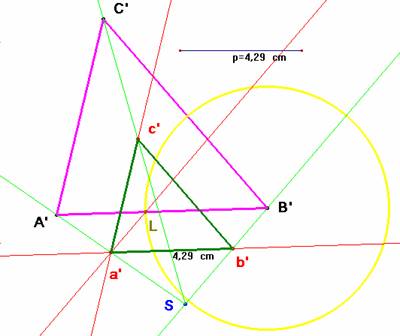
Dado el triángulo A'B'C', un segmento p y un punto S, para construir un triángulo homotético con centro de homotecia S y cuyo lado a'b' mida p se procede como se muestra en la figura.
Se toma una circunferencia con centro en B’ y radio B'L igual a la longitud del segmento p. Se une S con los vértices del triángulo y se traza por L una paralela a B’S que corta a A’S en el punto a’. El resto es fácil de ver en el dibujo.
Hacemos esto mismo con el triángulo A’B’C’ obtenido a partir de ABC. La figura siguiente muestra el resultado:
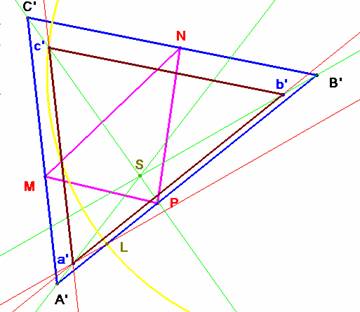
Ahora tenemos que girar adecuadamente el triángulo a’b’c’ hasta conseguir que sus lados pasen por los vértices de MNP y con ello habremos resuelto el problema.
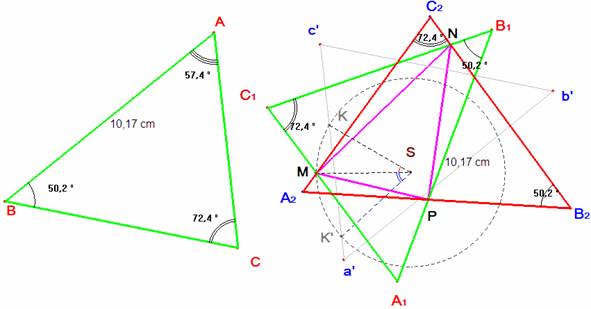
Trazamos con centro S una circunferencia que pasa por M. Intercepta en el lado a’c’ dos puntos K y K’. Un giro con centro S que transforme el punto K en M nos da el triángulo A1B1C1. Si el giro pasa de K’ a M se obtiene el triángulo A2B2C2.
Se obtienen dos soluciones en general para el problema propuesto.