Propuesto por Jean-Louis AYME ( Lycée Lislet Geoffroy, 97400 St.-Denis,) Île de la Réunion, France.

Problema 455. Sean AA₁, BB₁, CC₁ las alturas de un triángulo acutángulo. Demostrar que los pies de las perpendiculares trazadas por C₁ a los segmentos AC, BC, AA₁ y BB₁ están alineados. C₁ es el punto que determina la recta de Miquel ( The Miquel line If point P lies on the circumcircle of triangle ABC and perpendiculars from it are dropped onto the sides of ABC, then the pedal triangle degenerates into a straight line, the so-called Simson line. In general, if point P lies on the circumcircle of triangle ABC and lines from it are drawn to the sides of ABC (suitably extended if necessary) to form fixed angles q with the sides, then the Miquel triangle degenerates into a straight line, which we shall call the Miquel line.) BHB₁ según el triángulo AA₁C. (profundización del problema 447 de esta revista)

Ayme, J.L. (2008): Comunicación personal.

El profesor Jean Louis Ayme edita una página web sobre geometría

Cita: De Villiers M. (2002): From nested Miquel triangles to Miquel distances. Math Gazette, Nov 2002, 86(507), pp.390-395.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (5 de abril de 2008)

SOLUCIÓN

ESTUDIO DE LA FIGURA

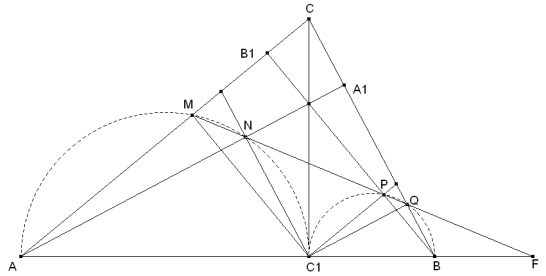
Sea M el pie de la perpendicular desde C₁ a CA, N el pie de la perpendicular desde C₁ a AA₁, P el pie de la perpendicular desde C₁ a BB₁ y Q el pie de la perpendicular desde C₁ a BC.

AMC₁ y C₁PB tienen los lados paralelos por ser perpendiculares a las mismas rectas; por tanto son homotéticos.

ANC₁ y C₁QB tienen los lados paralelos por ser perpendiculares a las mismas rectas; por tanto son homotéticos.

M y N están sobre el mismo círculo AMNC₁ por ser vértices opuestos a la hipotenusa en triángulos con la misma base AC₁.

P y Q están sobre el mismo círculo C₁PQB por ser vértices opuestos a la hipotenusa en triángulos con la misma base C₁B.

Pero los dos círculos anteriores son homotéticos en las mismas homotecias que los ángulos anteriores y en consecuencia los triángulos AMC₁, ANC₁ son respectivamente homotéticos a los triángulos C₁PB y C₁QB en la misma homotecia de centro F que es la intersección de MP con AB (o la intersección de NQ con BA).

Por lo tanto, si demostramos que F, P y Q están alineados; como también lo están F, P y M ( también F, Q y N); habremos demostrado que M, N, P, Q están alineados como pide el enunciado. Para demostrar la alineación de F, P, Q demostraremos que el ángulo ∠FQP es nulo

Por lo tanto los pies respectivos de las perpendiculares del enunciado están alineados.