Propuesto por Jean-Louis AYME ( Lycée Lislet Geoffroy, 97400 St.-Denis,) Île de la Réunion, France.

Problema 455.- Sean AA₁, BB₁, CC₁ las alturas de un triángulo acutángulo. Demostrar que los pies de las perpendiculares trazadas por C₁ a los segmentos AC, BC, AA₁ y BB₁ están alineados. C₁ es el punto que determina la recta de Miquel (The Miquel line if point P lies on the circumcircle of triangle ABC and perpendiculars from it are dropped onto the sides of ABC, then the pedal triangle degenerates into a straight line, the so-called Simson line. In general, if point P lies on the circumcircle of triangle ABC and lines from it are drawn to the sides of ABC (suitably extended if necessary) to form fixed angles q with the sides, then the Miquel triangle degenerates into a straight line, which we shall call the Miquel line.) BHB₁ según el triángulo AA₁C. (profundización del problema 447 de esta revista).

Ayme, J.L. (2008): Comunicación personal.

El profesor Jean Louis Ayme edita una página web sobre geometría

Cita: De Villiers M. (2002): From nested Miquel triangles to Miquel distances. Math Gazette, Nov 2002, 86(507), pp. 390-395.

Solución.-

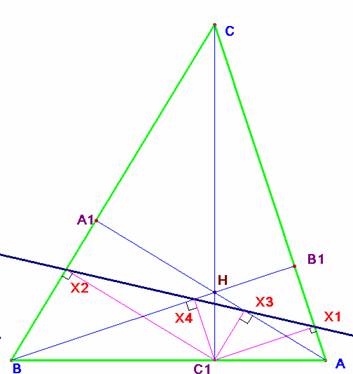
La alineación de los pies de las perpendiculares ya quedó probada en el problema 447. Por ello vamos directamente a la segunda parte.

Se trata de probar que BHB₁ es una recta de Miquel desde el punto C₁ para el triángulo AA₁C, o sea, que las rectas C₁B₁, C₁B y C₁H cortan a los lados AC, CA₁ y AA₁ con un mismo ángulo. C₁B₁A₁ es el triángulo órtico de ABC.

Los triángulos que se fijan en las esquinas de ABC sabemos que son semejantes a él. Esto ya se ha visto y utilizado en ocasiones anteriores (nº 17).

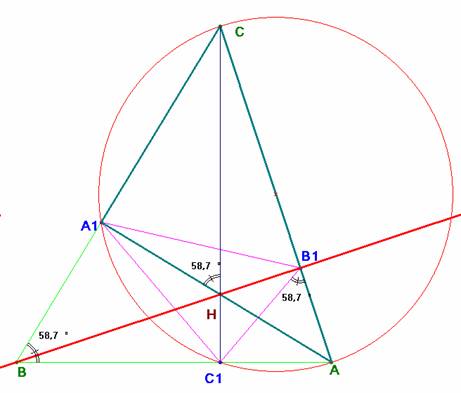
Así, por ejemplo, AC₁B₁ se corresponde por semejanza con ABC, siendo el ángulo en B₁ igual al ángulo B. Por otra parte el ángulo A₁HC también es igual al ángulo B por tener sus lados perpendiculares a los de éste. En resumen, se verifica lo que pretendíamos demostrar: BHB₁ es una recta de Miquel desde el punto C₁ para el triángulo AA₁C y ángulo B.