IN  MEMORIAM

 

JUAN  CARLOS  SALAZAR  (?-2008)

 

 

EL  PROBLEMA  456

 

 

 

Jean-Louis  AYME

 

 

 

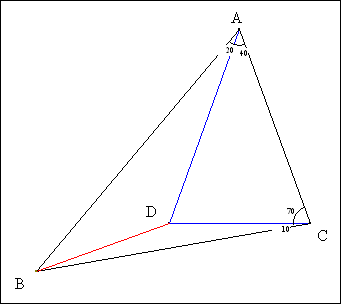
En el triangulo ABC, D es un punto interior tal que

<BCD = 10°,  <ACD = 70°,  <BAD = 20°,  <CAD = 40°.

Probar que BD es perpendicular a AC. [1]

 

 

 

Scolie :                                  <ADC = 70° ; en conséquence, le triangle ADC est isocèle en A.

 

 

Contexte :                             ce triangle isocèle ayant un angle de 40° au sommet, nous suggère que ce

                                               problème 456 correspond au thème "Adventitious Angles"[2] ou "Mahatma's Puzzle"[3] ou

encore "Tantale"[4].

 

 

Note historique :                 le premier nom a été donné en 1922 par Edward M. Langley[5], le deuxième par par la revue Mathematical Spectrum[6] en 1995 et le dernier par J. L. Heilbron[7] en 1998.

                                               L'origine de ce thème remonte à l'année 1916 où le célèbre problème de Langley a été posé à "Entrance Examination for Peterhouse and Sidney Sussex Colleges" à Cambridge. Depuis de nombreuses variations sur ce thème ont été présentées[8].

 

 

Technique choisie :            elle s'inspire de celle utilisée en 1951 par S. T. Thompson de Tacoma (Washington, États-unis) pour la résolution du problème de Langley[9].

 

 

 

 

UN  LEMME  FÉDÉRATEUR

 

 

 

VISUALISATION

 

 

Figure :

 

 

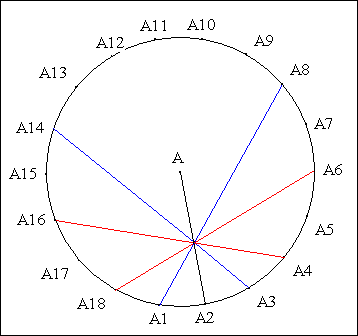
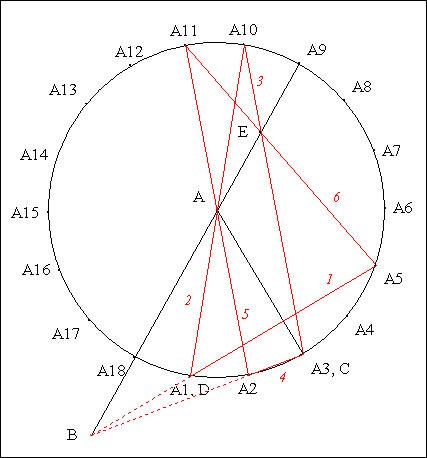
Traits :                  0                             un cercle,

                               A                            le centre de 0

                et            A1, A2,..., A18        les sommets du 18-gone régulier inscrit dans 0.

 

Donné :                 (A1A8), (A3A14), (A4A16), (A18A6) concourent sur (AA2).

 

 

VISUALISATION

 

 

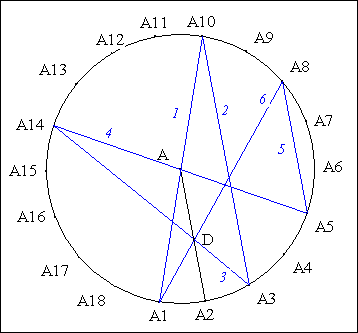
·   Scolie :             (AA2), (A3A10), (A5A8) sont parallèles entre elles.

 

·   Notons             D             le point d'intersection de (A1A8) et (A3A14).

 

·   D'après "L'équivalence d'Aubert-MacKensie" (Cf. Annexe 1),           

(1)          (AD) est la pascale de l'hexagone cyclique A1A10AA3A14A5A8A1

(2)          (AD) // (A5A8)   ou encore   (AD) // (AA2).

 

 ·   D'après le postulat d'Euclide,                     (AD) = (AA2).

 

·   Conclusion partielle :                                  A, D et A2 sont alignés.

 

 

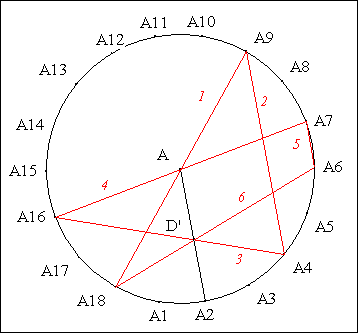
·   Scolie :             (AA2), (A4A9), (A6A7) sont parallèles entre elles.

 

·   Notons             D'            le point d'intersection de (A4A16) et (A6A18).

 

 

·   D'après "L'équivalence d'Aubert-MacKensie" (Cf. Annexe 1),           

(1)          (AD') est la pascale de l'hexagone cyclique A18A9A4A16A4A6A18

(2)          (AD') // (A4A9).

 

·   D'après le postulat d'Euclide,                      (AD') = (AA2).

 

·   Conclusion partielle :                                  A, D' et A2 sont alignés.

 

 

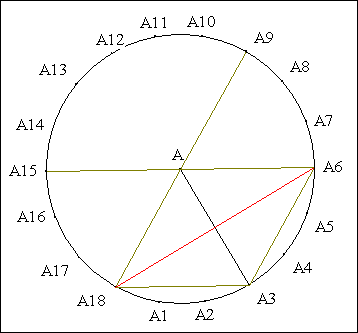
·   Scolies :                           (1)           (A3A18) // (A6AA15)

                                               (2)           (A3A6)  // (A9AA18)

                                               (3)           (AA18)  = (AA6).

 

·   Le quadrilatère AA18A3A6 est un losange.

 

·   Conclusion partielle :   (A6A18) est la médiatrice de [AA3]   ou encore   (A6A18)  (AA3).  

 

 

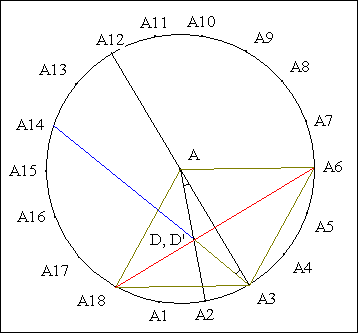
·   Scolies :           (1)           D est le point d'intersection de (AA2) et (A3A14)

(2)           <A2AA3 = <A12A3A14   (= 20°).

 

·   Le triangle DA3A est isocèle en D.

 

·   D'après le théorème de la médiatrice,         D est sur (A6A18) ;

     en conséquence,                                           D et d' sont confondus.

 

·   Conclusion :   (A1A8), (A3A14), (A4A16), (A18A6) concourent sur (AA2).

 

 

 

Commentaire :    ce lemme, dans son principe, fédère le thème "Adventitious angles".

 

 

 

 

LA  PREUVE

 

 

 

 

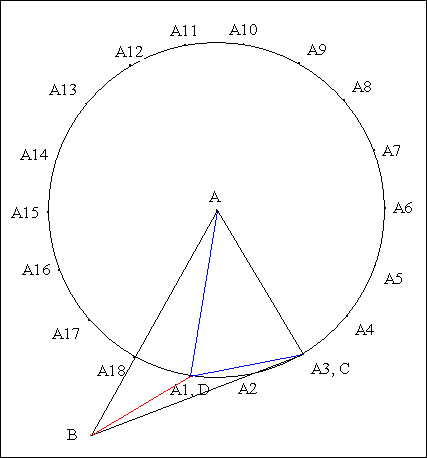
·   Immergeons notre figure dans celle du lemme précédent.

 

·   Scolies :           (1)           C et A3 sont confondus

                               (2)           D et A1 sont confondus

                               (3)           B, A2, C sont alignés.

 

 

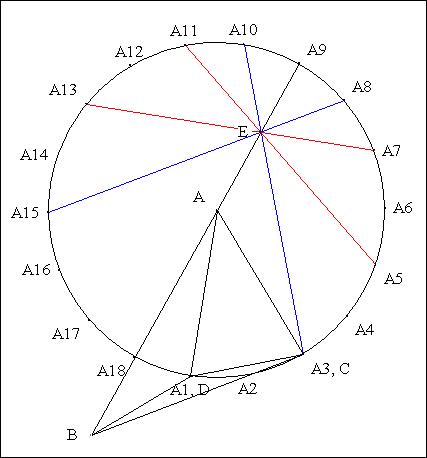
·   D'après le lemme,            (A8A15), (A10A3), (A11A5), (A7A13) concourent sur (AA9).

 

·   Notons             E             ce point de concours.

 

·   Scolie :             A, B, E, A9, A18 sont alignés.

 

 

·   Scolies :           (1)           A1, A, A10 sont alignés

                               (2)           A2, A, A11 sont alignés.

 

·   D'après Pascal "Hexagramma mysticum" (Cf. Annexe 2),     

     (AE) est la pascale de l'hexagone cyclique A5A1A10A3A2A11 ; en conséquence,             (A1A5) passe par B.

 

·   Nous avons :                                                                 (A1A5B)   //  (A6A18) ;

     d'après le lemme,                                                           (A6A18)    (AA3) ;

     d'après l'axiome IVa des perpendiculaires,                (A1A5B)  (AA3)   ou encore          (BA1) (AA3).

 

·   Conclusion :   "BD es perpendicular a AC".  

 

 

 

 

À  

 

son  épouse  Milagros

 

 

 

C'est le 16 avril 2004, que Juan Carlos[10] a pris contact avec moi, par mail, à partir de Puerto Ordaz (Venezuela).

Ce contact qui n'a jamais été rompu, nous a permis d'échanger nos travaux géométriques. Je sais qu'il a occupé avec talent les fonctions de coach de l'équipe vénézuelienne pour les I.M.O. et partager avec enthousiasme les dicussions ax seins des groupes Hyacinthos et Mathlinks.

Le dernier contact que j'ai eu avec lui, date du 9 septembre 2007 ; il m'écrivait :

 

"I am in Maputo, Mozambique, and I am working in Isolux, Spain Electrical Company, as electrician engineer, my profession. I am retired from my sweet geometry…".

 

Il décède le dimanche 30 mars 2008 en Afrique du Sud et est enterré le lundi 7 avril au Venezuela dans la religion catholique.

 

Qu'il repose en paix.

Jean-Louis

 

 

 

 

ANNEXE

 

 

 

1.  L'équivalence d'Aubert-MacKensie

 

 

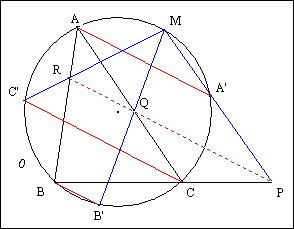
Traits :                 ABC                       un triangle,

                               0                             le cercle circonscrit à ABC,

                               A', B', C'                 trois points de 0 tels que (AA'), (BB') et (CC') soient parallèles entre elles,

                               M                           un point,

                et            P, Q, R                    les point d'intersection de (MA') et (BC),  (MB') et (CA),  (MC') et (AB).

 

Donné :                 M est sur 0     si, et seulement si,     (PQR) est une ménélienne de ABC, parallèle à (AA').

 

 

Scolie :                  la visualisation nécessaire est de Paul Aubert[11] et suffisante de M'Kensie[12].

 

 

2.  Hexagramma mysticum[13]

 

 

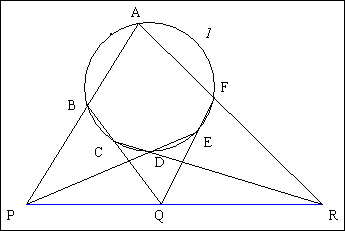
Traits :                  1                             un cercle,

                               ABCDEF               un hexagone tels que les points A, B, C, D, E soient sur 1,

et            P, Q, R                   les points d'intersection de (AB) et (DE), (BC) et (EF), (CD) et (FA).

 

Donné :                 F est sur 1             si, et seulement si,               les points P, Q et R sont alignés.


[1]              Communiqué au site "Laboratorio virtual de triangulos con cabri" de Ricardo Barroso en 2004 ;

http://www.personal.us.es/rbarrosocabri/html

L'énoncé a été reformulé par l'auteur.

[2]              En français, Aventure angulaire.

[3]              Titre donné en Inde à des personnalités spirituelles de premier plan.

[4]              Dans la Mythologie, Tantale était le roi de Phrygie qui, pour avoir offensé les dieux, fut précipité dans les Enfers et condamné à

une faim et à une soif dévorantes.

[5]              Langley, Adventitious Angles Problem, Mathematical Gazette, 11 (1923) 321-323.

[6]              Mathematical Spectrum vol. 27 (1995-97) 7, 65-67.

[7]              Heilbron J. L., Geometry civilised, Clarendon Press, Oxford (1998) 292-295.

[8]              Rike T., An intriguing Geometry Problem, Berkeley Math Circle (2002) ;

Diamond R. A. & Georgiou G. R., Triangles and Quadrilaterals Revisted Part 2: The solution, Mathematics in School 30, 1

(November 2001) 11-13.

[9]              Langley E. M., A problem, Mathematical Gazette, 11 (1922) 173.

[10]             Salazar J. C., Google : Applicaciones del Teorema de Desargues ; Concurrencias y Colinealidades.

 

[11]             Aubert P., Généralisation du problème de Pascal donnant neuf points en ligne droite, Nouvelles Annales (1899).

[12]             M'Kensie, Journal de Mathématiques Spéciales de Longchamps (1887) 201.

[13]             Pascal B. (1640)