In memoriam
Dedicado a Juan Carlos Salazar, colaborador y amigo. Descanse en paz.
Dedicado a Milagros.
Problema 456
En el triángulo ABC, D es un punto interior tal que: <ABD=10º, <CBD=70º,<ACD=20º <BCD=40º Probar que AD es perpendicular a BC.
Juan Carlos Salazar (2004): Comunicación personal.
Solución del director de la revista.
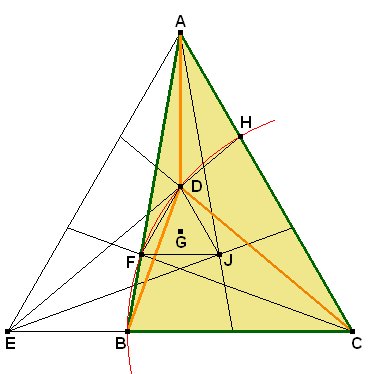
Olvidamos por el momento el enunciado y consideramos la figura como un triángulo equilátero en el que se han trazado las trisectrices de sus ángulos, siendo AB una de ellas y D el punto donde se cortan otras dos. Se formará el triángulo equilátero DFJ. Este triángulo será homotético a ABC, con centro de homotecia el baricentro G de ambos triángulos. La recta AD es perpendicular a FJ y a EC.
El triángulo CBF es isósceles ya que ÐFBC=180º-60º-40º=80º y ÐBCF=20º. Por simetría, también CHD es isósceles, y, por simetría también CB=CH. Por tanto, CB=CF=CD=CH y los puntos B, F, D, H están en una circunferencia con centro C. En ella tenemos el ángulo inscrito ÐFBD =(1/2) ÐFCD = 10º.
Resulta entonces que los puntos A, B, C, D cumplen el punto de partida del problema, por lo que AD es perpendicular a BC.
Ricardo Barroso Campos
Didáctica de
Universidad de Sevilla.