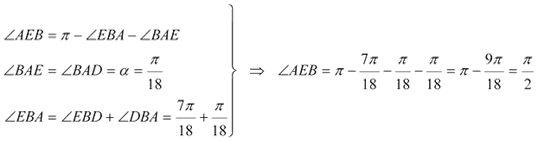In memoriam
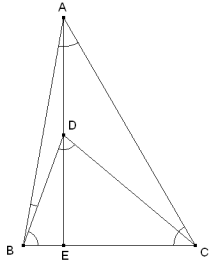
Problema 456. En el triángulo ABC, D es un punto interior tal que: ∠ABD = 10°, ∠CBD = 70°, ∠ACD = 20°, ∠BCD = 40°. Probar que AD es perpendicular a BC. Juan Carlos Salazar (2004): Comunicación personal Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (4 de abril de 2008) |
|
SOLUCIÓN |
|
Dibujamos el enunciado
Debemos hallar el ángulo ∠BAD al que denominaremos α. Aplicamos el teorema de los senos al triángulo ABD donde el enunciado nos lleva a
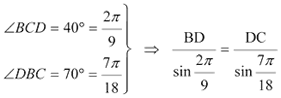
en el triángulo BDC
en el triángulo ACD
Multiplicando las tres igualdades obtenidas miembro a miembro, obtenemos
Simplificando
y teniendo en cuenta la igualdad trigonométrica
nos queda
Introducimos ahora el ángulo doble
y simplificando, obtenemos la ecuación1
Si observamos la ecuación 1, podemos ver para que valor de α obtenemos una igualdad de senos compatible con la ecuación y así evitamos la resolución numérica de la ecuación. Por ejemplo, una condición sería
valor que sustituido, de nuevo, en la última ecuación confirma que
Llamemos E al punto de encuentro de AD con BC. Tomamos ahora el triángulo AEB y calculamos el ángulo ∠AEB
que nos demuestra que AE es perpendicular a BC y por tanto AD y BD son perpendiculares (c.q.d.). |
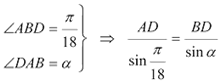
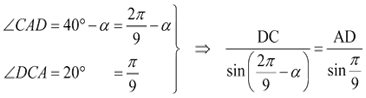
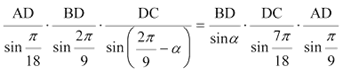
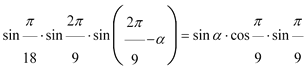 .
.