Problema 456.- (In memoriam. Dedicado a Juan Carlos Salazar. Descanse en paz).

En el triángulo ABC, D es un punto interior tal que: , , , . Probar que AD es perpendicular a BC.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Consideremos un triángulo semejante al triángulo ABC dado, cuyos ángulos son , y . Consideremos también un punto D en el interior del triángulo ABC tal que y . Entonces y el triángulo CBD es isósceles con .

Supondremos, sin pérdida de generalidad, que . Entonces tenemos que y la proyección del punto D sobre el lado BC medida desde el vértice B será

. [1]

Por otra parte, aplicando el teorema de los senos al triángulo ABC tenemos que

y la proyección del punto A sobre el lado BC medida desde el vértice B es

[2]

Finalmente, para demostrar que AD es perpendicular al lado BC, basta con relacionar [1] y [2] y utilizar relaciones trigonométricas elementales (relaciones entre ángulos complementarios) para demostrar la siguiente identidad

[3]

Mediante las fórmulas trigonométricas de transformación de productos en sumas es inmediata la relación

por lo que al sustituir en la expresión [3] tenemos

y después de simplificar, utilizar las fórmulas trigonométricas del ángulo doble y la fórmula de transformación , nos queda

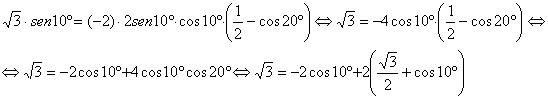
lo que demuestra la proposición propuesta.