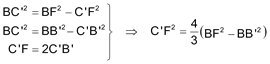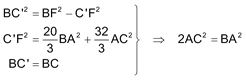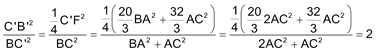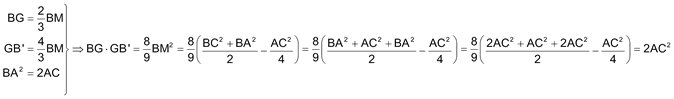|
Dedicado a Juan Carlos Salazar por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid. Problema 457. Hallar la relación que deben verificar los catetos del triángulo ABC, rectángulo en A, para que al construir el triángulo ABC´ simétrico con respecto al lado AB, el triángulo ACB´ con B´ simétrico de B, respecto al punto medio de AC, los triángulos BC´B´ y GB´C´, sean semejantes al triángulo ABC siendo G el baricentro de este último triángulo. Romero, J.B. (2008): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (5 de abril de 2008) |
|
SOLUCIÓN |
|
|
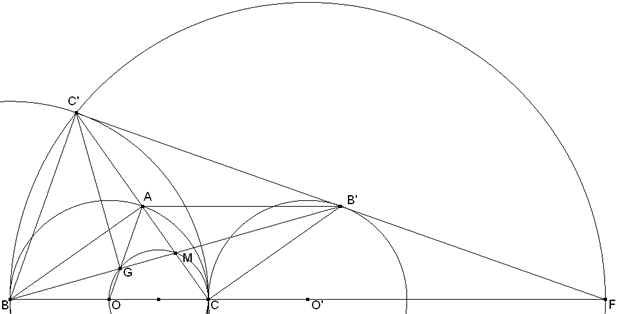
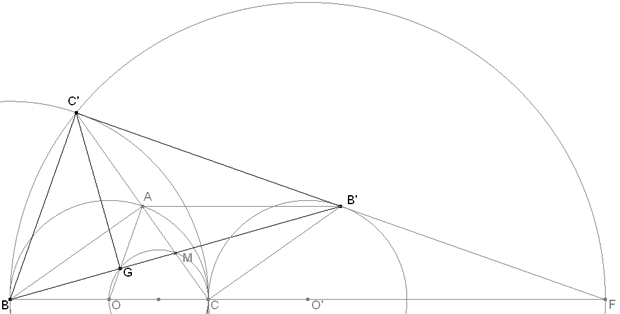
ESTUDIO DE LA FIGURA - EL PUNTO C'
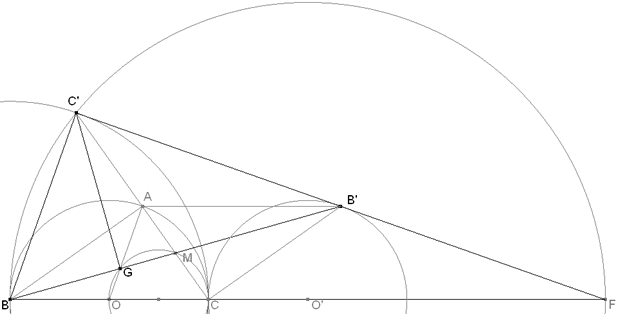
Sea BC la hipotenusa del triángulo; entonces A está sobre el círculo de diámetro BC. Si O es el punto medio de BC y M es el punto medio de AC, G es la intersección de AO y BM. Al ser BAC rectángulo en A, CA es perpendicular a BA y por tanto C’ también es el simétrico de C respecto de A; es decir, C’ es la imagen de A en una homotecia de centro C y razón 2. Ello indica que el lugar geométrico de C’, al variar A, es el círculo de centro B y radio BC. Como M es el punto medio de AC y de BB’, el cuadrilátero ABCB’ es un paralelogramo con el lado AB’ paralelo e igual a BC; pero BC es fijo, de donde B’ es la imagen de A por una traslación de vector BC; en consecuencia, el lugar de B’ al variar A es un círculo de centro O’ y radio O’C=OC ya que OO’=BC en magnitud y sentido. El círculo lugar de C’ es entonces la imagen del círculo lugar de B’ en una homotecia de razón 2, la recta C’B’ pasará por un punto fijo F sobre BC, su centro de homotecia, pero como estos dos círculos tienen un solo punto en común que es C, se cumple que BF/O’F=2 que nos lleva a que BO’=O’F y así BC=⅔BO’. Pero como BC’ tiene que formar ángulo recto con C’B’, y C’B’ pasa por F, C’ ha de estar sobre el círculo de diámetro BF=3BC. EL TRIÁNGULO ABC’ ABC y ABC’ tienen dos lados iguales (AC=AC’ y AB común) y el ángulo que comprenden igual (∠BAC=∠BAC’=recto) y por lo tanto no sólo son semejantes, además son congruentes (de razón 1). ABC’ es la imagen de ABC por una simetría de eje AB. POR CONSTRUCCIÓN SIEMPRE ES SEMEJANTE. Por lo tanto este triángulo no determina ninguna proporción entre los catetos de ABC. EL TRIÁNGULO ACB’ Hemos visto que ABCC’ es un paralelogramo, entonces ABC y ACB’ tienen tres lados iguales (BA=B’C, BC=B’A y CA común). Por lo tanto los triángulos son semejantes de lados iguales; pero en esta semejanza C y A se intercambian y M es un punto fijo, lo que significa que la razón es negativa. ACB’ es la imagen de ABC por una simetría de centro M (o una semejanza de centro M y razón -1). POR CONSTRUCCIÓN SIEMPRE ES SEMEJANTE. Por lo tanto este triángulo no determina ninguna proporción entre los catetos de ABC. EL TRIÁNGULO BC’B’
Aprovechando que BC’F y BC’B’ son triángulos rectángulos
Hemos visto que BF = 3BC y como BB’ = 2BM y BM es la mediana por el vértice B en el triángulo ABC que es rectángulo
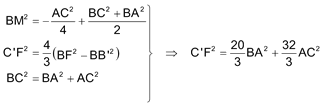
y entrando, de nuevo, en la ecuación de BC’²
Por lo tanto la relación de catetos pedida es Relación = Esta relación en el triángulo BC’B’ nos lleva a que
Como ABC y BC’B’ tienen la misma relación de catetos y ambos son rectángulos, entonces son semejantes. EL TRIÁNGULO GC’B’ Recordando ahora el teorema de la altura para un triángulo rectángulo (ver el teorema 1. 3 del nº 400 extra en estas mismas páginas de RICARDO BARROSO)
Teniendo en cuenta que ABC es rectángulo, que BM es una mediana, que G es el baricentro y la relación de catetos
y la el segmento GC' es
entonces como en un triángulo rectángulo, la altura sobre la hipotenusa es media proporcional de los segmentos en que divide a ésta, C’G es la altura de BC’B’ y por tanto perpendicular a BB’ con lo que GC’B’ es rectángulo en G y también semejante a BC’B’; pero BC’B’, acabamos de ver que es semejante a ABC, concluimos que GC’B’ es semejante con ABC. |