Problema 457.- Dedicado a Juan Carlos Salazar. (Propuesto
por J. B. Romero Márquez, profesor colaborador de
Hallar la relación que deben
verificar los catetos del triángulo ABC,
rectángulo en A, para que al
construir el triángulo ABC´ simétrico
con respecto al lado AB, el triángulo
ACB´ con B´ simétrico de B
respecto del punto medio de AC, los
triángulos C´B´B y GB´C´, sean semejantes al triángulo ABC, siendo G el baricentro de este último triángulo.
Resolución: (Vicente Vicario García, I.E.S. El Sur,
Huelva)
Utilizaremos la geometría de coordenadas
con el vértice A del ángulo recto en
el origen de coordenadas y los catetos situados sobre los semiejes positivos de
abscisas y ordenadas. Supondremos, sin pérdida de generalidad, los vértices 
, 
, 
. Son inmediatas entonces las coordenadas 
, 
y 
.
Para que los triángulos C´B´B y GB´C´ sean semejantes al triángulo ABC es necesario que sean rectángulos y para esta situación sólo
tenemos dos posibilidades: O bien 
, o bien 
. Consideremos la primera posibilidad, es decir. Entonces es necesario también que 
. Veamos ahora que esta posibilidad es posible y bajo que
circunstancias. Para ello tenemos que
; 
[1]
Además como 
y 
con lo que ,
con la suposición de [1]. Veamos también que, además de
ángulos rectos, se mantiene la semejanza. Para ello basta observar que, bajo
las condiciones de [1] tenemos que
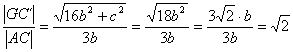
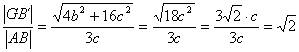
luego,
efectivamente los triángulos C´B´B , GB´C´ y ABC son semejantes con la condición 
. Finalmente, podemos ver que la otra posibilidad, bajo las condiciones del problema, es imposible, ya que se
llega a un absurdo 
y entonces 
.
---oooOooo---