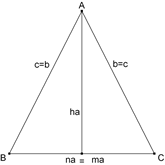
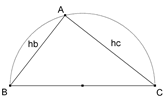
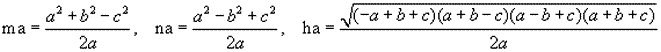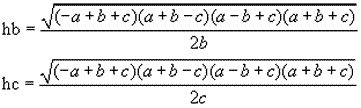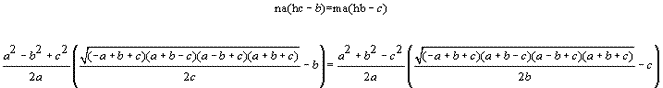De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 460. Caracterizar a todos los triángulos de lados a, b, y, c, alturas ha, hb, hc, respectivamente, y con a = ma+na, siendo ma, y na, las proyecciones ortogonales de los lados b y c, sobre a, respectivamente, y verificando: na (hc-b) = ma (hb-c).

Romero, J. B. (2006): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (22 de abril de 2008)

Solución

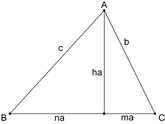
Observando la figura obtenemos las siguientes ecuaciones

que resueltas nos proporcionan

y análogamente

Introduciendo estos valores en la condición del enunciado, obtenemos

y simplificando

que nos proporciona cuatro posibilidades

(i)

Todos los triángulos isósceles de base a

(ii)

Es un triángulo degenerado en que la suma de dos lados es igual a la base

(iii)

Se limita a un punto.

(iv)

Esta condición se reduce a

Es un triángulo rectángulo de base a.

También podíamos haber elevado al cuadrado los miembros de la ecuación última y habríamos obtenido