Problema 460

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 460

Caracterizar a todos los triángulos de lados a, b, y, c, alturas h_a,h_b,h_c, respectivamente,

y con a = m_a+n_a, siendo m_a, y n_a, las proyecciones ortogonales de los lados b y c, sobre a, respectivamente, y  verificando :              n_a( h_c-b)= m_a(h_b-c).

Romero, J. B. (2006): Comunicación personal.

Solución de Ricard Peiró:

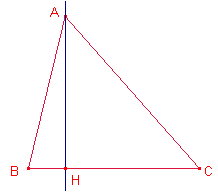
Sea el triángulo .

Sea , altura del triángulo, , .

Supongamos que , .

Aplicando razones trigonométricas a los triángulos rectángulos , :

, .

Aplicando el teorema del coseno al triángulo :

, . Simplificando:

, . Dividiendo las dos expresiones:

(1)

Por hipótesis, .

Calculando el área del triángulo :

, entonces:

. Entonces:

(2)

Igualando las expresiones (1) y (2):

.

.

.

.

.

.

y por la desigualdad triangular, .

Entonces, , es decir, el triángulo es isósceles, .

Supongamos que . .

Por hipótesis, , entonces, .

Por ser el triángulo , rectángulo . Aplicando el área del triángulo:

, entonces,

, entonces, , lo que es absurdo ya que .

Análogamente si , no hay triángulo posible.

Supongamos que , entonces, , por tanto, . Por tanto, también se consigue la igualdad .