Problema 460.- (Propuesto por J. B. Romero Márquez,
profesor colaborador de
Caracterizar a todos los
triángulos de lados 
y alturas 
, respectivamente, y con 
siendo 
y 
las proyecciones ortogonales de los lados b y c
sobre a, respectivamente, y
verificando 
.
Resolución: (Vicente Vicario García, I.E.S.
El Sur, Huelva)
Consideremos un triángulo arbitrario ABC y la notación habitual. A partir de la relación requerida y sustituyendo los valores correpondientes tenemos que
Utilizando el teorema de los senos
generalizado 
, 
, 
y después de simplificar llegamos a
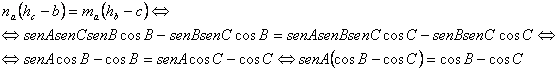
Para esta última igualdad tenemos dos posibilidades o caracterizaciones
(a)
Si 
. Por otra parte, es inmediato comprobar que para cualquier
triángulo rectángulo en A se cumple
la condición ya que 
y 
.
(b)
Si 
y el triángulo es isósceles. En este caso también es fácil
comprobar que se cumple la caracterización ya que 
, 
y 
.