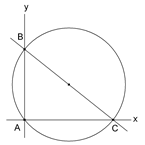
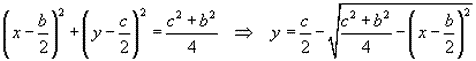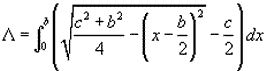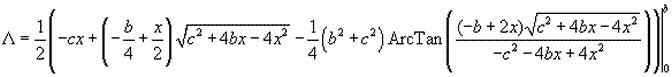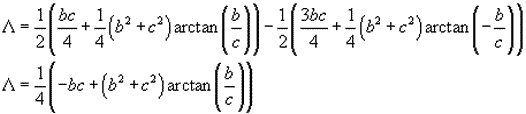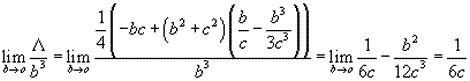De investigación. Propuesto por Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva

Problema 461. En un triángulo rectángulo ABC, el cateto AB es constante de longitud c, siendo el otro cateto AC de longitud variable b. En la circunferencia circunscrita al triángulo, sea Λ el área del menor de los segmentos circulares determinados por el cateto AC. Hallar .Lim b->0 Λ/b³

Vicario, V. (2008): Comunicación personal (Tomado de Las Oposiciones de Andalucía de 1996 (anotación de Ricard Peiró))

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (22 de abril de 2008)

Solución

Observando la figura vemos que la ecuación de la circunferencia es

teniendo en cuenta los signos, el área pedida queda como

y resolviendo

Sustituyendo los límites obtenemos

y recordando el desarrollo limitado hasta tercer grado de arctan(x) en el entorno de x=0

nos queda