Problema 461

En un triángulo rectángulo ABC, el cateto AB es constante de longitud c, siendo el otro cateto AC de longitud variable b. En la circunferencia circunscrita al triángulo, sea el área del menor de los segmentos circulares determinados por el cateto AC. Hallar ..-

Vicario, V. (2008): Comunicación personal (Tomado de Las Oposiciones de Andalucía de 1996 (anotación de Ricard Peiró))

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Sea O el centro de la circunferencia circunscrita al triángulo ABC. Sabemos por el teorema de Thales que dicho punto corresponde al punto medio de la hipotenusa BC. Además, los triángulos ABO y AOC son isósceles pues . Sean entonces y , con . Se tiene entonces que . También se observa fácilmente que las áreas de los triángulos AOB y AOC son iguales. Por tanto, denotando, determinando el área del sector circular AOC, el área del triángulo AOC, aplicando el teorema de Pitágoras, y la relación trigonométrica , tenemos que

y el límite pedido es entonces

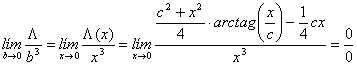
Determinaremos este límite de dos formas distintas. En la primera aplicaremos reiteradamente la regla de L´Hôpital y en la segunda, utilizaremos desarrollos en serie infinita.

(a)

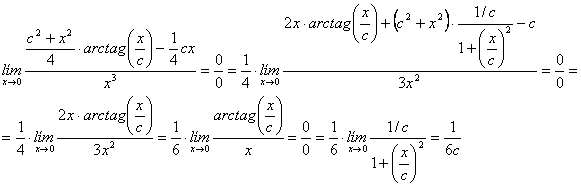
(b) Utilizaremos el desarrollo en serie de la función en torno al origen

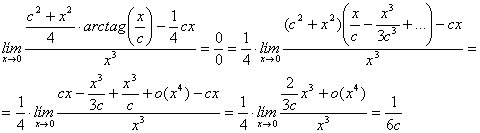
Nota: La sustitución directa en el límite anterior de por la expresión , conduce a error ya que esta operación no es lícita. De hecho, si proseguimos con el límite tendríamos el valor erróneo siguiente para el propuesto

.
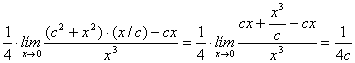