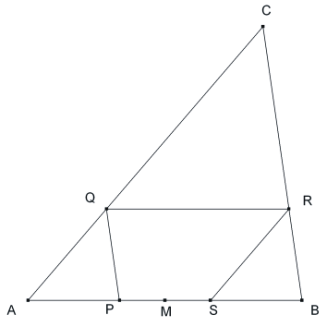
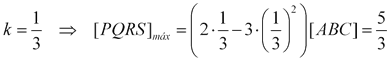Para el aula .

Problema 462. - 198. Consideremos un triángulo ABC de área 5. Para cada punto P de AB más cercano de A que de B, consideremos Q de AC, R de BC y S de AB tal que PQ sea paralela a BC, QR a AB y RS a AC. Determinar el valor máximo obtenido por el área del cuadrilátero PQRS.

REVISTA DO PROFESSOR DE MATEMÁTICA 47, 2001

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (23 de abril de 2008)

Solución

Observando la figura obtenemos la siguiente expresión para el área [PQRS]

Por tener los lados paralelos, los triángulos ABC, APQ, SBR y QRC son semejantes. Es más, por tener la misma altura, los triángulos APQ y SBR son congruentes. Sean k y r las razones de semejanza de esos triángulos con ABC

Pero por paralelas entre paralelas

y de aquí

Y como en una semejanza la razón de áreas es igual al cuadrado de la razón de semejanza, tenemos

Introducido todo en la expresión del área buscada

Esta expresión presenta un máximo si k = ⅓