Problema 462

Considerem el triangle d’àrea 5.

Per a cada punt P del costat més a prop A que de B, considerem els punts Q del costat , R de i S de tal que siga paral·lel a , a i a . Determineu el valor màxim obtingut per l’àrea del quadrilàter PQRS.

Solució de Ricard Peiró:

Siga M el punt mig del costat , siga P un punt del segment .

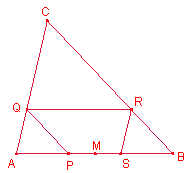Siga .

Notem que els triangles , són iguals.

BRQP és un paral·lelogram. Aleshores, .

Si dos triangles semblants, les àrees són proporcionals al quadrat de la raó de semblança.

Els triangles , són semblants, aleshores:

, aleshores, .

Els triangles , són semblants, aleshores:

, aleshores, .

El màxim de l’àrea del quadrilàter PQRS s’assoleix en el mínim de la suma d’àrees:

.

.

Considerem la paràbola , el mínim s’assoleix en l’eix de simetria de la paràbola:

.

Aleshores, l’àrea màxima del quadrilàter PQRS s’assoleix quan i és:

.
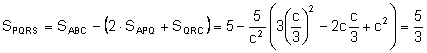