Problema 462

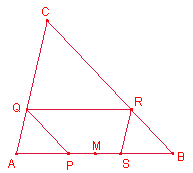
198. Consideremos un triángulo  ABC  de área 5.

Para cada punto P de AB más cercano de A que de B, consideremos Q de AC, R de BC y S de AB tal que PQ sea paralela a BC, QR a AB y RS a AC. Determinar el valor máximo obtenido por el área del cuadrilátero PQRS.

REVISTA DO PROFESSOR DE MATEMÁTICA 47, 2001

Solución de Ricard Peiró:

Sea M el punto medio del lado , sea P un punto del segmento .

Sea .

Notemos que los triángulos , son iguales.

BRQP es un paralelogramo. Entonces, .

Si dos triángulos semejantes, las áreas son proporcionales al cuadrado de la razón de semejanza.

Los triángulos , son semejantes, entonces:

, entonces, .

Los triángulos , son semejantes, entonces:

, entonces, .

El máximo del área del cuadrilátero PQRS se alcanza en el mínimo de la suma de áreas:

.

.

Consideremos la parábola , el mínimo se alcanza en el eje de simetría de la parábola:

.

Entonces, el área máxima del cuadrilátero PQRS se alcanza cuando y es:

.
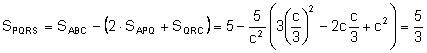