Problema 462.- Consideramos un triángulo ABC de área 5. Para cada punto P de AB, más cercano de A que de B, consideramos Q de AC, R de BC y S de AB tal que PQ sea paralela a BC, QR a AB y RS a AC. Determinar el valor máximo obtenido para el área del cuadrilátero PQRS.

(Revista do profesor de Matemática, 47, 2001).

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo del problema denotaremos [XYZ] como el área del triángulo XYZ y [XYZW] el área del cuadrilátero XYZW. Debido a la construcción es inmediato que los triángulos APQ, CQR, BRS y ABC son semejantes entre sí.

Denotaremos por k la razón de semejanza entre los triángulos APQ y ABC de manera que, respetando las condiciones del problema

con

Es inmediato también observar que si k es la razón de semejanza entre los triángulos APQ y ABC, entonces es la razón de semejanza entre los triángulos CQR y ABC y, de nuevo, k vuelve a ser la razón de semejanza entre BRS y ABC. Por tanto, tenemos que

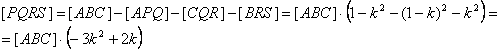
Por último, es inmediato observar que la función alcanza su máximo (absoluto) en y vale , con lo que el área máxima del cuadrilátero PQRS pedido es

Esto viene a decirnos que debemos trisecar el lado AB y así, después de seguir el proceso, obtendremos el cuadrilátero de área máxima.