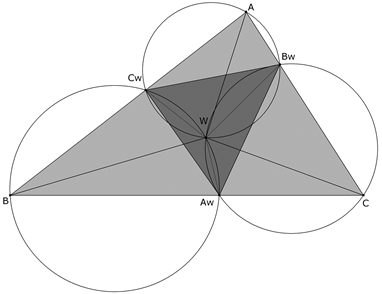
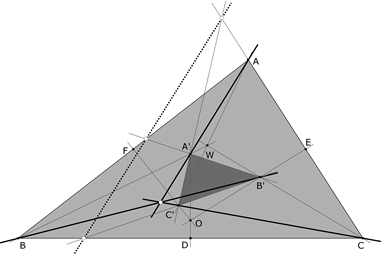
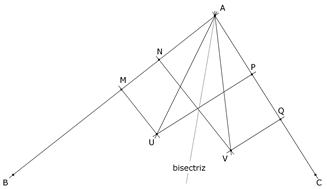
De investigación. Propuesta de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona) Problema 463 Sea ABC un triángulo cualquiera. Sea AwBwCw un triángulo variable e inscrito en ABC con Aw sobre BC, Bw sobre CA y Cw sobre AB. (1) Demostrar que los círculos circunscritos a los triángulos ABwCw, AwBCw, AwBwC tienen un punto común W. (2) Demostrar que para que W sea fijo, los distintos triángulos AwBwCw deben ser semejantes entre sí. Supongamos que los triángulos AwBwCw varían permaneciendo semejantes al triángulo original ABC de forma que la semejanza sea directa y el homólogo de A se desplace sobre AB (A→Cw, B→Aw, C→Bw). (3) Demostrar que W es el centro de semejanza entre ABC y AwBwCw. (4) Demostrar la identidad de los ángulos ÐWAB, ÐWBC y ÐWCA. En esta situación, llamamos A’ al punto de intersección de BW con la mediatriz de BC, B’ al punto de intersección de CW con la mediatriz de CA y C’ al punto de intersección de AW con la mediatriz de AB. (5) Demostrar que ABC y A’B’C’ están en perspectiva. (6) Demostrar que si por los vértices del triángulo ABC trazamos paralelas a los lados de A’B’C’, esas rectas son concurrentes en el círculo circunscrito. Análogamente, demostrar que las perpendiculares por los vértices de ABC a los lados de A’B’C’ también son concurrentes sobre el círculo circunscrito. Demostrar que estos dos puntos de concurrencia son diametralmente opuestos. (7) Demostrar que W y el circuncentro O del triángulo ABC son concíclicos con A’, B’ y C’. (8) Demostrar que A’B’C’ es inversamente semejante al triángulo ABC. Hallar la razón de esta semejanza inversa. (9) Demostrar que el punto simediano K del triángulo ABC es concíclico con A’, B’ y C’. Demostrar que K es diametralmente opuesto a O en el círculo circunscrito a A’B’C’. Pedret, J.M. (2008): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (5 de abril de 2008) |
|
APARTADO (1) |
|
Sea ABC un triángulo cualquiera. Sea AwBwCw un triángulo variable e inscrito en ABC con Aw sobre BC, Bw sobre CA y Cw sobre AB. (1) Demostrar que los círculos circunscritos a los triángulos ABwCw, AwBCw, AwBwC tienen un punto común W. |
|
Demostraremos que la intersección de dos de los círculos está sobre el tercero. Sea W el punto de intersección de los círculos AwBCw y AwBwC. Por el ángulo del arco capaz, el ángulo ÐAwWCw es (π-B). Por el ángulo del arco capaz, el ángulo ÐAwWBw es (π-C). Entonces el ánguloÐBwWCw es (2π-ÐAwWCw-ÐAwWBw) = 2π-(π-B)-(π-C) = B+C = (π -A). Lo que nos indica que W está en el arco BwCw opuesto al ángulo A en el círculo ABwCw. En consecuencia W es un punto común a los tres círculos circunscritos a los triángulos ABwCw, AwBCw, AwBwC. |
|
APARTADO (2) |
|
Sea ABC un triángulo cualquiera. Sea AwBwCw un triángulo variable e inscrito en ABC con Aw sobre BC, Bw sobre CA y Cw sobre AB. (2) Demostrar que para que W sea fijo, los distintos triángulos AwBwCw deben ser semejantes entre sí. |
|
Veamos que la posición de W sólo depende de los ángulos de los dos triángulos del enunciado. ÐBWC = ÐBWAw+ÐAwWC = ÐBCwAw+ÐAwBwC = (π-ÐCwAwB-B)+(π-C-ÐCAwBw) = (2π-B-C)-(ÐCwAwB+ÐCAwBw) = (2π-B-C)-(π-ÐCwAwBw) = (π-B-C)+ÐCwAwBw = A+Aw Análogamente ÐCWA = B+Bw y ÐAWB = C+Cw y por tanto, hemos demostrado que la posición de W sólo depende de los ángulos del triángulo original y del inscrito. Si los distintos triángulos AwBwCw permanecen semejantes entre sí, los ángulos Aw, Bw, Cw permanecen fijos y como los ángulos A, B, C son fijos; tenemos que los ángulos ÐBWC = A+Aw , ÐCWA = B+Bw y ÐAWB = C+Cw son fijos y en consecuencia, el punto W es fijo. |
|
APARTADO (3) |
|
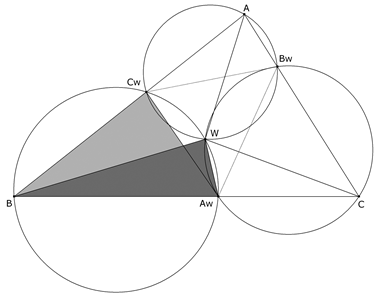
Supongamos que los triángulos AwBwCw varían permaneciendo semejantes al triángulo original ABC de forma que la semejanza sea directa y el homólogo de A se desplace sobre AB (A→Cw, B→Aw, C→Bw). (3) Demostrar que W es el centro de semejanza entre ABC y AwBwCw. |
|
En el caso de la semejanza directa entre ABC y AwBwCw se pueden dar tres casos: (i) Aw → A, Bw → B y Cw → C con ÐBWC = 2A, ÐCWA = 2B, ÐAWB = 2C. (ii) Aw → B, Bw → C y Cw → A con ÐBWC = A+B, ÐCWA = B+C, ÐAWB = C+A. (iii) Aw → C, Bw → A y Cw → B con ÐBWC = A+C, ÐCWA = B+A, ÐAWB = C+B. En el caso de la semejanza inversa entre ABC y AwBwCw se pueden dar tres casos más: (iv) Aw → A, Bw → C y Cw → B con ÐBWC = 2A, ÐCWA = B+C, ÐAWB = C+B. (v) Aw → B, Bw → A y Cw → C con ÐBWC = A+B, ÐCWA = B+A, ÐAWB = 2C. (vi) Aw → C, Bw → B y Cw → A con ÐBWC = A+C, ÐCWA = 2B, ÐAWB = C+A. Recordemos que un lugar geométrico del centro de una semejanza es el círculo que contiene dos puntos homólogos y el punto de intersección de dos rectas homólogas a las que pertenecen los dos puntos homólogos mencionados. En los seis casos, los tres puntos que definen cada círculo son dos puntos homólogos en esa semejanza y el punto de intersección de dos rectas también homólogas y que contienen los dos puntos anteriores. Teniendo en cuenta los dos párrafos anteriores, concluimos que W es el centro de esa semejanza y como tal un punto fijo de esa transformación. En la figura 3 podemos ver el caso (ii), Cw y A son homólogos y Bw es la intersección de BwCw con CA. |
|
APARTADO (4) |
|
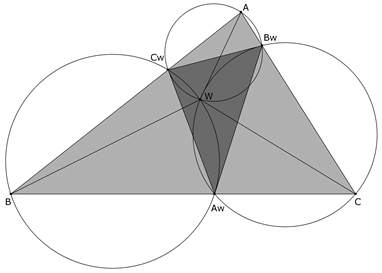
Supongamos que los triángulos AwBwCw varían permaneciendo semejantes al triángulo original ABC de forma que la semejanza sea directa y el homólogo de A se desplace sobre AB (A→Cw, B→Aw, C→Bw). (4) Demostrar la identidad de los ángulos ÐWAB, ÐWBC y ÐWCA. |
|
El caso que nos ocupa, (A→Cw, B→Aw, C→Bw), es el caso (ii) del apartado (3) en el que los ángulos que forma W con los vértices A, B, C son ÐBWC = A+B = (π-C), ÐCWA = B+C = (π-A) y ÐAWB = C+A = (π-B). Podemos ver la identidad de los ángulos ÐWAB, ÐWBC y ÐWCA ya que en el triángulo AWB, π = ÐBWA+ÐWAB+ÐABW = (π-B)+ÐWAB+(B-ÐWBC) = π+(ÐWAB-ÐWBC) de donde obtenemos que ÐWAB = ÐWBC y repitiendo el mismo proceso con los triángulos BWC y CWA obtenemos respectivamente ÐWBC = ÐWCA y ÐWCA = ÐWAB. Podemos pues escribir ÐWAB = ÐWBC = ÐWCA = w. Podemos comprobar, de paso, que el círculo ABwCw es tangente a CwAw, ya que por la semejanza el ángulo entre el segmento BwCw y CwAw es A y coincide con el ángulo capaz A de ese segmento BwCw inscrito en ese círculo. Análogamente, el círculo AwBCw y el círculo AwBwC son tangentes a AwBw, y a BwCw respectivamente. |
|
APARTADO (5) |
|
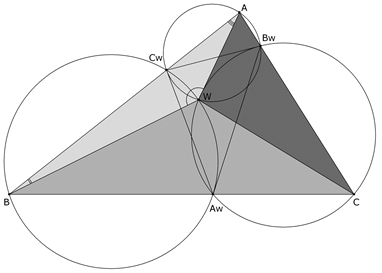
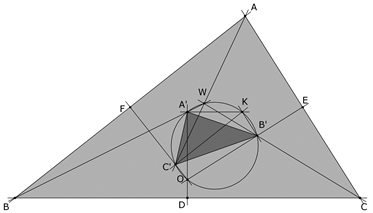
En esta situación, llamamos A’ al punto de intersección de BW con la mediatriz de BC, B’ al punto de intersección de CW con la mediatriz de CA y C’ al punto de intersección de AW con la mediatriz de AB. (5) Demostrar que ABC y A’B’C’ están en perspectiva. |
|
Para demostrar que ABC y A’B’C’ son perspectivos, demostraremos que AA’, BB’ y CC’ son concurrentes. Atendiendo a la igualdad de ángulos demostrada en el apartado (4) y como D, E y F son los puntos medios de los lados de ABC; los triángulos ABC’, BCA’, CAB’ son semejantes e isósceles y su ángulo en la base es w; de donde en el triángulo BCA’,por ejemplo, BA’ = A’C. El teorema de los senos en el triángulo BAA’ lleva a senBAA’/BA’ = senA’BA/A’A. El teorema de los senos en el triángulo A’AC lleva a senA’AC/A’C = senA’CA/A’A. Dividiendo miembro a miembro, obtenemos senBAA’/senA’AC = senA’BA/senA’CA. Pero ÐA’BA = ÐWBA = π-ÐBAW-ÐAWB = π-w- (π-B) = (B-w) y análogamente ÐA’CA = (C-w) con lo que obtenemos senBAA’/sen A’AC = sen (B-w)/sen (C-w). Y del mismo modo senCBB’/sen B’BA = sen (C-w)/sen (A-w) y senACC’/sen C’CB = sen (A-w)/sen (B-w) y multiplicando estas tres últimas igualdades [senBAA’·senCBB’·senACC’]/[senA’AC·senB’BA·senC’CB]=[sen(B-w)·sen(C-w)·sen(A-w)]/[sen(C-w)·sen(A-w)·sen(B-w)]=1. Pero esta igualdad no es más que la expresión trigonométrica de la condición de concurrencia de las cevianas AA’, BB’ y CC’ según el teorema de Ceva aplicado al triángulo ABC. Gracias a Desargues, como resultado adicional, podemos decir que los puntos de intersección de los lados AB con A’B’, BC con B’C’ y CA con C’A’ están alineados. |
|
APARTADO (6) |
|
En esta situación, llamamos A’ al punto de intersección de BW con la mediatriz de BC, B’ al punto de intersección de CW con la mediatriz de CA y C’ al punto de intersección de AW con la mediatriz de AB. (6) Demostrar que si por los vértices del triángulo ABC trazamos paralelas a los lados de A’B’C’, esas rectas son concurrentes en el círculo circunscrito. Análogamente, demostrar que las perpendiculares por los vértices de ABC a los lados de A’B’C’ también son concurrentes sobre el círculo circunscrito. Demostrar que estos dos puntos de concurrencia son diametralmente opuestos. |
|
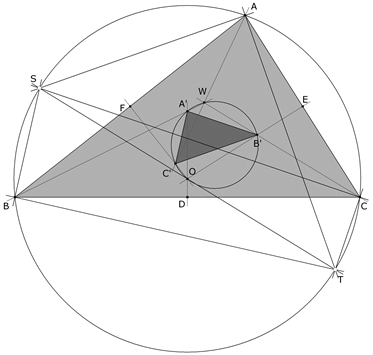
Si las paralelas a B’C’ por A y a C’A’ por B se encuentran en S. Entonces ÐASB = π-ÐA'C'B' = π-ÐACB, por tanto S está sobre el círculo circunscrito. Análogamente las intersecciones de la paralela a A'B' por C con las dos paralelas anteriores también está sobre el círculo circunscrito; pero esas dos paralelas ya cortan al cículo circunscrito en S y por tanto la paralela a A'B' por C también pasa por S. Si las perpendiculares a B’C’ por A y a C’A’ por B se encuentran en T. Entonces ÐATB =ÐA'C'B' = ÐACB, y por tanto T está sobre el círculo circunscrito. Análogo al caso de las paralelas, la perpendicular a A'B' por C también pasa por T. AS y AT son perpendiculares, por lo que el ángulo ÐSAT es recto; pero S, A y T están sobre el círculo circunscrito, entonces ST es un diámetro de ese círculo. |
|
APARTADO (7) |
|
En esta situación, llamamos A’ al punto de intersección de BW con la mediatriz de BC, B’ al punto de intersección de CW con la mediatriz de CA y C’ al punto de intersección de AW con la mediatriz de AB. (7) Demostrar que W y el circuncentro O del triángulo ABC son concíclicos con A’, B’ y C’. |
|
Primero veremos que W, O, A’ y B’ son concíclicos y para ello demostraremos que el cuadrilátero WA’OB’ es inscriptible. Como OA’ es perpendicular a BC y OB’ lo es a CA, el ángulo ÐA’OB’ es igual a C; pero ÐA’WB’=ÐBWC que, como hemos visto en el apartado (4), es (π-C); por lo tanto dos ángulos opuestos en el cuadrilátero son suplementarios y en consecuencia, el cuadrilátero es inscriptible; por lo que los puntos W, O, A’ y B’ son concíclicos. Por un razonamiento análogo, W, O, B’ y C’ son concíclicos y en consecuencia A’ y C’ son concíclicos con W, O, B’. En definitiva, los puntos W y O son concíclicos con A', B' y C'. |
|
APARTADO (8) |
|
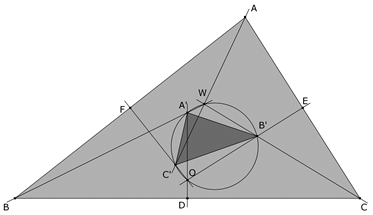
En esta situación, llamamos A’ al punto de intersección de BW con la mediatriz de BC, B’ al punto de intersección de CW con la mediatriz de CA y C’ al punto de intersección de AW con la mediatriz de AB. (8) Demostrar que A’B’C’ es inversamente semejante al triángulo ABC. Hallar la razón de esta semejanza inversa. |
|
Hemos visto en el apartado anterior que los ángulos ÐB’C’A’ y ÐB’OA’ están inscritos en el mismo arco y en consecuencia son iguales; pero también, en ese apartado, hemos visto que el ángulo ÐB’OA’ es igual a C; podemos concluir que ÐB’C’A’ es igual a C. Del mismo modo, podemos concluir que el ángulo ÐA’B’C’ es B y que ÐC’A’B’ es A. Es decir, los triángulo ABC y A’C’B’ tienen los mismos ángulos y por tanto son semejantes. Basta ver que el orden de dos de los ángulos está intercambiado para concluir que la semejanza es inversa. Recordemos que en un triángulo cotA·cotB + cotB·cotC + cotC·cotA = 1 y como hemos visto en el apartado (4) ÐBWC =(π-C), ÐCWA = (π-A), ÐAWB = (π-B) y también ÐWAB = ÐWBC = ÐWCA = w de lo que podemos deducir que cot(w) = cotA + cotB + cotC. Si descomponemos el área de A’B’C’ en las áreas (con signo) de los triángulos cuyos vértices son O y dos de los vértices de A’B’C’, obtenemos [A’B’C’] = [OA’B’] + [OB’C’] + [OC’A’]. Y como hemos visto que los ángulos ÐB’C’A’ y ÐB’OA’ son iguales hallamos, por ejemplo, que [OA’B’]/[ABC] = (½·OA’·OB’·senB'OA')/(½·CA·CB·senB'C'A') = (OA’·OB’)/(CA·CB) = ((OD-A’D)·(OE-B’E))/(CA·CB); siendo D el pie de la mediatriz de BC; pero por ser el ángulo en el centro del círculo circunscrito ÐBOD es igual al ángulo capaz de la cuerda BC y por tanto ÐBOD = A y de aquí cotA = OD/DB = OD/(½·CB), además hemos visto más arriba que tan(w) = DA’/DB = DA’/(½·CB). En consecuencia, hallando ecuaciones análogas para las otras mediatrices y ángulos [OA’B’]/[ABC] = ((½·CB· cotA-½·CB·tan(w))·((½·CA· cotB-½·CB·tan(w)))/(CA·CB) = ¼ (cotA-tan(w))·(cotB-tan(w)); y sumando las relaciones para los tres triángulos obtenemos [A’B’C’]/[ABC] = ¼(cotA-tan(w))·(cotB-tan(w)) + ¼(cotB-tan(w))·(cotC-tan(w)) + ¼(cotC-tan(w))·(cotA-tan(w)) =¼(cotA · cotB +cotB · cotC +cotC · cotA - 2·( cotA+cotB+cotC)· tan(w)+3tan²(w)) = ¼ (1-2cot(w)·tan(w) + 3 tan²(w)) = ¼ (3 tan²(w)-1) pero la razón de áreas es el cuadrado de la razón de semejanza y teniendo en cuenta que el signo de [A’B’C’] es distinto que el de [ABC], por ser la semejanza inversa, tenemos que la razón pedida es ½(1-3tan²(w))½ |
|
APARTADO (9) |
|
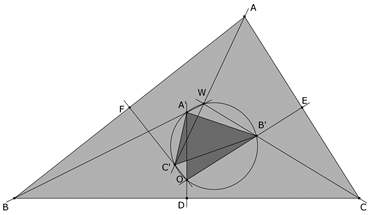
En esta situación, llamamos A’ al punto de intersección de BW con la mediatriz de BC, B’ al punto de intersección de CW con la mediatriz de CA y C’ al punto de intersección de AW con la mediatriz de AB. (9) Demostrar que el punto simediano K del triángulo ABC es concíclico con A’, B’ y C’. Demostrar que K es diametralmente opuesto a O en el círculo circunscrito a A’B’C’. |
|
Rectas conjugadas isogonales Dos rectas AU y AV son conjugadas isogonales respecto de un ángulo ÐBAC, cuando forman ángulos iguales con la bisectriz del ángulo. (Ver también Útiles Simples para la Resolución de Problemas de Triángulos, problema extra 400 - 0.6 Cevianas isogonales) Una propiedad de los puntos sobre rectas isogonales Si desde dos puntos U y V, situados respectivamente sobre dos rectas conjugadas isogonales respecto de un ángulo dado ÐBAC, trazamos perpendiculares UM y VN al lado AB del ángulo y perpendiculares UP y VQ al lado AC; entonces se cumple que UM·VN = UP·VQ. (Ver también Útiles Simples para la Resolución de Problemas de Triángulos, problema extra 400 - 4.1 Cevianas isogonales)
Como los ángulos ÐBAU y ÐCAV son iguales, UM/AU = VQ/AV y por la perpendicularidad, AU/UP = AV/VN; multiplicando estas dos igualdades miembro a miembro, obtenemos UM/UP = VQ/VN y por tanto UM·VN = UP·VQ. Una propiedad del punto simediano K Las perpendiculares desde K a los lados del triángulo son proporcionales a los lados.
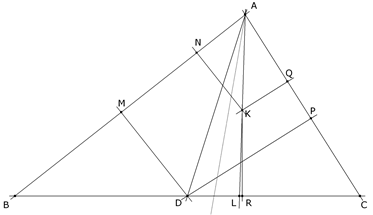
Sabemos que K está sobre las simedianas, conjugadas isogonales de las medianas, y llamamos D al punto medio de BC y L la intersección de la simediana con BC. En estas condiciones podemos tomar a D y K como los puntos U y V del párrafo anterior. Según la propiedad anterior, podemos escribir que DM·KN = DP·KQ; pero como AD es la mediana desde A, las áreas de los triángulos BAD y DAC coinciden y ½·AB·DM = ½·CA·DP. Combinando las dos últimas igualdades, obtenemos que DM/DP = KQ/KN = CA/AB. Si R es el pie de la perpendicular desde K al lado BC y repetimos este último procedimiento con la mediana y la simediana por el vértice B obtenemos KN/KR = AB/BC. Como queríamos probar, uniendo estos dos últimos resultados tenemos que KR/BC = KQ/CA = KN/AB Resolución del apartado (9)
Vamos a usar la propiedad anterior del punto simediano para trazarlo. Aprovecharemos, por ejemplo, las igualdades de los ángulos ÐWBC y ÐWCA , como hemos demostrado en el apartado (4). Como w = ÐWBC = ÐWCA y ½π = ÐODB = ÐOEC, los triángulos A’BD y B’CE tienen tres ángulos iguales y por tanto son semejantes y se cumple que A’D/BD = B’E/CE; pero BD = ½·BC y CE = ½·CA y en consecuencia A’D/BC = B’E/CA que reordenado nos da que B’E/A’D = CA/BC. Pero A’D es la distancia de la perpendicular desde A’ al lado BC y por lo tanto, la distancia entre el lado BC y una paralela a este lado por el punto A’. B’E es la perpendicular desde B’ al lado CA y por lo tanto, la distancia entre el lado CA y una paralela a este lado por el punto B’; entonces un punto K, que se encuentre en la intersección de ambas paralelas, posee la proporción de distancias a los lados BC y AC igual a la proporción de los lados; ya que si Q y R son los pies de las perpendiculares desde K a los lados, KQ/KR = B’E/A’D; pero como hemos visto en el párrafo anterior, B’E/A’D = CA/BC y por tanto KQ/KR = CA/BC; y esa es la propiedad que caracteriza a K como el punto simediano. Ahora sólo nos falta probar que K es concíclico con A’, B’, C’ y para ello demostraremos que el caudrilátero KA’C’B’ es inscriptible. Como KA’ es paralela a BC y KB’ es paralela a CA el ángulo ÐA’KB’ es igual a (π-C) el suplementario del ángulo ÐBCA y como hemos visto en el apartado (8) el ángulo ÐA’C’B’ es C lo que nos indica que dos ángulos opuestos de ese cuadrilátero son suplementarios y por tanto el cuadrilátero es inscriptible; con lo que concluimos que el punto simediano K es concíclico con los puntos A’, B’ y C’. Que OK es el diámetro es fácil de demostrar, en nuestro caso, ya que O también está en el círculo A'B'C' y el ángulo ÐOA’K es recto por ser A’O perpendicular a BC y A’K paralela a BC. |
|
NOTAS |
|
El círculo circunscrito a A’B’C’ recibe el nombre de círculo de Brocard. En bibliografía diversa, el círculo de Brocard suele definirse como el círculo de diámetro OK y luego es habitual demostrar que los puntos de Brocard están sobre ese círculo. También es habitual definir A’, B’, C’ como las intersecciones de las mediatrices de los lados con el círculo de Brocard. El triángulo A’B’C’ recibe el nombre de primer triángulo de Brocard. Lo que se intenta con este enunciado es ver un procedimiento en sentido reciproco o contrario a los habituales para establecer el círculo y el primer triángulo de Brocard. Es decir, partir de la definición de un triángulo y determinar que su círculo circunscrito es el círculo de Brocard. Para ello, hemos visto que sobre el círculo circunscrito a los puntos A’B’C’ se encuentra un punto de Brocard, el circuncentro y el punto simediano. La construcción del punto simediano demuestra que OK es un diámetro de este círculo. Para hallar el otro punto de Brocard, basta con considerar la semejanza en la que el punto homólogo de A se desplaza por AC. El lector interesado puede demostrar multitud de resultados siguiendo la línea del enunciado. Tal como se ha procedido aquí, se han construido A’, B’, C’ respectivamente sobre BW, CW, AW y en consecuencia no es necesario demostrar que AC’, BA’, CB’ son concurrentes en un punto W (punto de Brocard). Hemos demostrado que AA’, BB’ y CC’ son concurrentes: El punto de concurrencia es el conjugado isotómico de K en el triángulo ABC. Si KA’, KB’, KC’ encuentran a los lados de ABC en los puntos D1 y D2, E1y E2, F1 y F2; los lados del triángulo F1D1E1 son paralelos a AW, BW y CW; y los lados de E2F2D2 son paralelos a AW’, BW’, CW’ donde W’ sería el otro punto de Brocard. Los puntos W y K son los puntos de Brocard del triángulo F1D1E1; los puntos W’ y K del triángulo E2F2D2. La recta WW’ es perpendicular al diámetro OK. Hemos visto que las paralelas por los vértices de ABC a los lados del primer triángulo de Brocard son concurrentes. El punto S de concurrencia recibe el nombre de punto de Steiner. Hemos visto que las perpendiculares desde los vértices de ABC a los lados del primer triángulo de Brocard son concurrentes. El punto de concurrencia recibe el nombre de punto de Tarry. Así hasta multitud de resultados de gran interés que pueden establecerse, como se ha visto, por medio de métodos sencillos de geometría. |