Problema 464

Nuevo

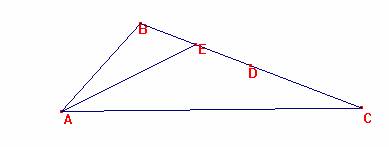
ABC es un triángulo en el que BC= 2 AB. Sean D el punto medio de BC, y E el punto medio de BD. Demostrar que AD es la bisectriz del ángulo CAE.

Aref, M.N., Wernick,W. (1968): Problems &Solutions in Euclidean Geometry. Dover Publications, Inc, New York. (pag. 4)

Solución del director

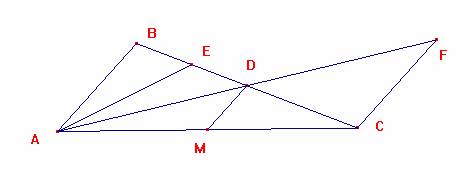
Tracemos la recta AD y la paralela a AB por C que se cortarán en F.

Tracemos M punto medio de AC, y DM.

Es 2DE=DC.

Es 2DM=AB, y 2ED=DB=AB. Luego DM=DE.

Es AB=BD, por lo que el triángulo ABD es isósceles en B, y si <ABD=b, es

<BDA=90º-b/2.

Por otra parte, debido a la construcción hecha, es: <ADM=<AFC.

El triángulo DFC tiene DC=CF=AB, y <DCF=<ABD, por lo que es isósceles, siendo

<DCF=b, <CFD=<CDF=90º-b/2.

Por lo que <MDA=<CFD=90º-b/2.

Así los triángulos ADE y ADM tienen <EDA=<MDA=90-b/2, y ED=DM=a/2, así como el lado AD común. Luego <EAD=<MAD, cqd.

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla.