Problema 464

és un triangle tal que . Siguen D el punt mig de i E el punt mig de . Demostreu que és la bisectriu de l’angle .

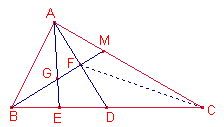Solució de Ricard Peiró:

. Aleshores, el triangle és isòsceles.

Siga F el punt mig de .

La recta BF talla el costat en el punt ;M.

és bisectriu de l’angle B. Aplicant la propietat de la bisectriu:

, . Aleshores:

.

Siga G la intersecció dels segments , , baricentre del triangle .

Per ser el triangle isòsceles, és perpendicular a .

Els triangles , són rectangles.

Dos triangles que tenen la mateixa altura les àrees són proporcionals a les bases.

Siga S l’àrea del triangle . Siga T l’àrea del triangle .

Els triangles , tenen la mateixa altura, aleshores:

, aleshores, .

Els triangles , tenen la mateixa altura, aleshores:

, aleshores, .

Els triangles tenen la mateixa altura, aleshores:

, aleshores, .

Els triangles tenen la mateixa altura, aleshores:

, aleshores, .

Les àrees dels triangles són iguals, aleshores:

, aleshores:

.

Aleshores, els triangles rectangles , són iguals.

Aleshores, , és bisectriu del triangle isòsceles .

Per tant, és la bisectriu de l’angle .

Solució amb Cabri:

Figura barroso464.fig

Applet created on 2/05/08 by Ricard Peiró with CabriJava