Problema 464.- ABC
es un triángulo en el que ![]() . Sea D el punto
medio de BC y E el punto medio de BD.
Demostrar que AD es la bisectriz del
ángulo CAE.
. Sea D el punto
medio de BC y E el punto medio de BD.
Demostrar que AD es la bisectriz del
ángulo CAE.
Aref, M.V. Wernick, W (1968).
Problems and Solutions in Euclidian Geometry. Dover
Publications, Inc,
Resolución: (Vicente Vicario García, I.E.S. El Sur,
Huelva)
Utilizaremos la notación habitual en la geometría del triángulo y resolveremos el problema mediante tres métodos diferentes.
1º Método: En virtud del teorema de Stewart aplicado al triángulo ABC con ceviana AE tenemos que
![]()
y después de
simplificar y teniendo en cuenta que ![]() , entonces queda
, entonces queda
![]()
Finalmente, como se tiene que
![]() y
y ![]()
se deduce (mediante
un sencillo argumento por reducción al absurdo que involucra el teorema de las
bisectrices interiores) que AD es la
bisectriz interior del ángulo ![]() en el triángulo CAE.
en el triángulo CAE.
---oooOooo---
2º Método: Es claro que según la construcción en el problema, AD es la mediana del triángulo ABC que parte del vértice A. Es bien sabido que la mediana en función de los lados está dada por (teorema de Apolunio)
![]()
y como![]() , la expresión anterior se reduce a
, la expresión anterior se reduce a
![]()
Por otra parte, AE es la mediana del triángulo ABD
que parte de A y en consecuencia,
conociendo la anterior expresión para AD,
y como![]() , tenemos que
, tenemos que
![]()
Sea ahora ![]() . Aplicando el teorema de los cosenos al triángulo DAC tenemos que
. Aplicando el teorema de los cosenos al triángulo DAC tenemos que
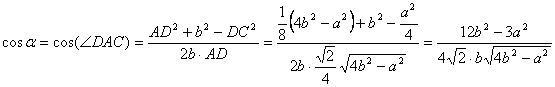
Sea ![]() . Aplicando el teorema de los cosenos al triángulo EAD y teniendo en cuenta que
. Aplicando el teorema de los cosenos al triángulo EAD y teniendo en cuenta que ![]() , tenemos que
, tenemos que
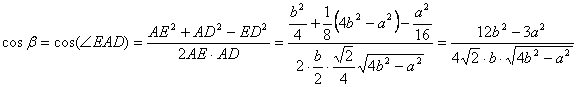
y en consecuencia
está claro que ![]() y AD es la bisectriz interior del ángulo
y AD es la bisectriz interior del ángulo ![]() en el triángulo CAE.
en el triángulo CAE.
---oooOooo---
3º Método: Recurrimos ahora a la geometría de
coordenadas. Sin pérdida de generalidad supondremos que ![]() ,
, ![]() y
y ![]() . Claramente tenemos que
. Claramente tenemos que ![]() y
y ![]() . Además, como
. Además, como ![]() , el vector AB (de
módulo 1) será
, el vector AB (de
módulo 1) será
![]() con la relación
con la relación ![]() ,
, ![]() [1]
[1]
Determinemos las ecuaciones de las rectas AC y AE y después la ecuación de la recta bisectriz interior AD.
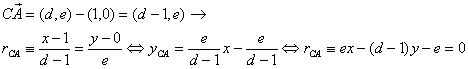
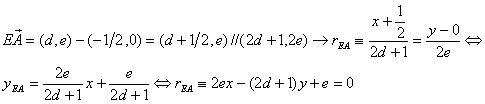
Por otra parte, sabemos que las
ecuaciones de las rectas bisectrices ![]() y
y ![]() (que son
perpendiculares entre sí) de las rectas
(que son
perpendiculares entre sí) de las rectas ![]() y
y ![]() analíticamente vienen
dadas por
analíticamente vienen
dadas por
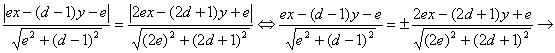
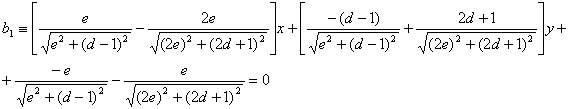
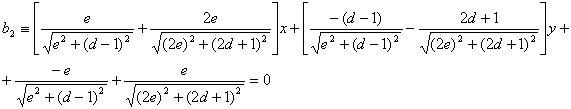
Podemos observar que la bisectriz ![]() pasa por el origen de
coordenadas puesto que claramente se tiene que, utilizando [1]:
pasa por el origen de
coordenadas puesto que claramente se tiene que, utilizando [1]:
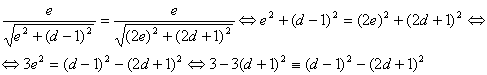
y en consecuencia
la recta bisectriz ![]() del ángulo
del ángulo ![]() pasa por el origen de
coordenadas, es decir, por el punto D,
y esto demuestra lo que queríamos.
pasa por el origen de
coordenadas, es decir, por el punto D,
y esto demuestra lo que queríamos.
---oooOooo---