Problema 466

En un triángulo rectángulo se conocen el perímetro 2p y la altura h correspondiente al ángulo recto y se pide obtener en función de p y h :
1) Los tres lados del triángulo y su área.
2) Condición para que el problema sea posible.
3) Los radios del círculo inscrito y del círculo ex-inscrito correspondiente al ángulo recto.
4) La distancia entre los centros de ambos círculos.
5) Construcción geométrica del triángulo dados p y h. (Para ello conviene usar el círculo ex-inscrito indicado)

Matemática Elemental (1933), Tomo II, N.1, Enero, propuesto en la ETSI de Caminos(1931) p.14, N. 39 .

Solución del director de la revista.

1) Supongamos construida la figura. Sea ABC el triángulo.

Construyamos el triángulo AB*C*, con B*BA y C*CA isósceles, <B*=<B/2, <C*=<C/2. <B*AC*=90+C*+B*=135º

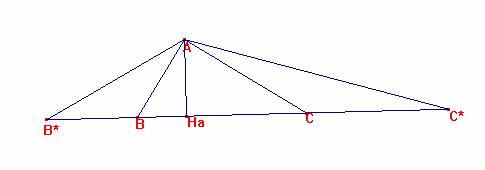
Es B*C*=2p, y AHa=h. Sea HaC*=x, B*Ha=2p-x.

Es: tg C*= h/x, tg B*=h/(2p-x).

tg B*= tg(45-C*), luego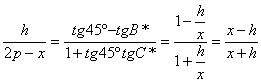

Resolviendo la ecuación tenemos que

Tomando el valor positivo de la raíz cuadrada, tenemos que:

.

.

Así podemos tener los ángulos B y C.

Por ello,

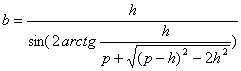
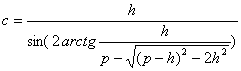
Las proyecciones de los catetos sobre la hipotenusa son:

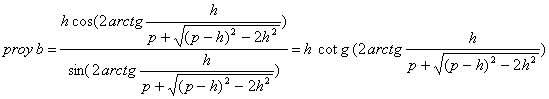
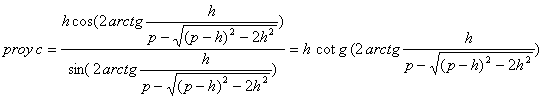
Luego la hipotenusa, a, mide:

Área del triángulo:

.

2) Condición para que el problema sea posible

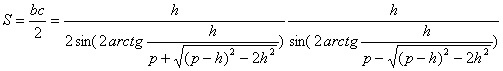El discriminante de la ecuación

ha de ser positivo,

3) Los radios del círculo inscrito y del círculo ex-inscrito correspondiente al ángulo recto.

.

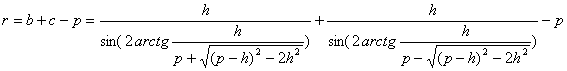r_a=p.

4) La distancia entre los centros de ambos círculos.

Es la diagonal del cuadrado de lado r_a-r =p-(b+c-p)=a

Luego es

5) Construcción geométrica del triángulo dados p y h. (Para ello conviene usar el círculo ex-inscrito indicado)

Dado 2p yh, trazamos la circunferencia con la cuerda 2p y arco capaz 135º.

A continuación trazamos la paralela a distancia h del segmento 2p.

Hay tres posibilidades:

i.- Que tal paralela no corte a la circunferencia.

No hay solución.

ii.- Que sea tangente a la circunferencia.

Hay una única solución, 135º 22.5º, 22.5º, isósceles que da lugar al 90º, 45º, 45º.

iii.- Que sea secante a la circunferencia, dando lugar a dos soluciones simétricas, siendo una de ellas A, C* B* 135º, C* y 45-C*, que, al tomar las mediatrices de AC* y AB* nos darán lugar a los vértices C y B del triángulo pedido en sus cortes con C*B*.